Глава VII. Проектирование несущих конструкции
§ 1. Расчет рандбалок
Как уже отмечалось, для зданий и сооружений в условиях Крайнего Севера широко применяются фундаменты в виде отдельных опор - стоек или свай, на которые передаются нагрузки от стен через рандбалки или ростверки.
В гражданском и промышленном строительстве свайные фундаменты обычно проектируются по упрощенной схеме, в которой сваи и ростверки рассчитываются самостоятельно, причем последние рассматриваются как балки (или плиты), опертые на сваи, и расчет их в этом случае ничем не отличается от расчета рандбалок.
При значительных горизонтальных нагрузках, когда совместный расчет свай и ростверков может дать ощутимый экономический эффект, проектирование свайных фундаментов рекомендуется производить по методам, принятым для гидротехнических сооружений [1].
Рандбалки применяются в промышленном и гражданском строительстве для одноэтажных и многоэтажных зданий при каркасных и бескаркасных схемах. В последнем случае через рандбалки передается нагрузка от всех этажей здания и его конструктивных элементов, включая перекрытие над подпольем.
Наряду с фундаментами рандбалки становятся, таким образом, наиболее ответственными конструктивными элементами зданий.
Продолжительность зимнего периода и низкие температуры на Крайнем Севере вызывают необходимость проектирования каменных конструкций с учетом (возведения их способом замораживания.
По мере возведения стен зданий этим! способом нагрузка на балку не только возрастает, но и перераспределяется, так-как жесткость кладки изменяется в зависимости от ее состояния (свежеуложенная, замороженная, оттаявшая, вызревшая).
В расчетах рандбалок можно ограничиться двумя основными случаями, характеризуемыми ниже.
В первом расчетном случае учитывается воздействие на рандбалку нагрузок от кладки стен, достигшей 28-дневной прочности после оттаивания, т. е. - соответствующих стадии эксплуатации здания. В этом случае для определения модуля упругости кладки следует принимать нормативное сопротивление сжатию и упругую характеристику кладки с учетом снижения расчетной марки раствора (против указанной в рабочих чертежах): на одну марку, если кладка велась при температуре наружного воздуха от -4 до -20 °С, и на две марки, если кладка велась при температуре ниже - 20 °С.
Во втором расчетном случае учитывается воздействие на рандбалку веса опирающихся на нее конструкций и монтажных нагрузок при наибольшей возможной степени готовности здания ко времени наступления первого оттаивания кладки. Степень готовности здания может быть принята по календарному плану работ и должна быть указана в рабочих чертежах.
Для определения модуля упругости оттаявшей кладки необходимо принимать нормативное сопротивление и упругую характеристику с учетом следующих указаний:
- в стадии оттаивания марка обыкновенных растворов на портландцементе, а также с химическими добавками принимается равной 2, если толщина стены или столба 38 см и более, а расчетная марка раствора, указанная на чертеже,- не менее 25. Во всех остальных случаях, а также при растворах на пуццолановом, шлакопортландском и других видах цементов, медленно твердеющих при пониженных температурах, прочность раствора в стадии оттаивания принимается равной нулю независимо от расчетной марки раствора, указанной в рабочих чертежах, толщины стен и столбов;
- сопротивление кладки стен из крупных кирпичных блоков, изготовленных при положительной температуре, принимается в стадии оттаивания кладки равным сопротивлению блоков с коэффициентом 0,6.
При расчетах на нагрузки по второму случаю необходимо учитывать, что рекомендуемое нормами проектирования каменных конструкций уменьшение пролета рандбалок установкой временных стоек (на период оттаивания и первоначального твердения кладки) при пучинистых грунтах недостаточно надежно. В расчете рандбалок кладка рассматривается как основание, упругие характеристики которого зависят от ее зрелости; задача сводится к вычислению усилий и расчету прочности рандбалки, работающей на изгиб, и кладки, работающей на смятие. Расчет рандбалок может производиться несколькими способами (табл. II-8).

Таблица II-8. Способы расчета рандбалок и условия их применения
По формулам указанных авторов оределяются усилия от равномерной нагрузки, а также от сосредоточенной, приложен ной на такой высоте, при которой она может быть заменена распределенной.
Усилия от нагрузок, которые не могут быть заменены равномерно распределенными, определяются отдельно по формулам и эпюрам распределения давления в кладке и суммируются с усилиями, полученными по способам табл. П-8.
Внешние силы, приложенные на уровне низа кладки, способные нарушить ее контакт с рандбалкой, следует передавать на самостоятельные балки.
Расчеты рандбалок сводятся к проверке предварительно принятых сечений и марок материалов. В изложении методов расчета приняты следующие обозначения:
q - интенсивность равномерно распределенной вертикальной нагрузки, приложенной к стене поверху или на Другом уровне, достаточно удаленном по высоте от рандбалки;
γоб - собственный вес единичного объема кладки;
R - реакция опоры однопролетной свободно лежащей рандбалки;
М - изгибающий момент;
Q - поперечная сила;
h - высота поперечного сечения рандбалки;
L - расчетный пролет, равный при коротких опорах (реакции которых можно рассматривать сосредоточенными) расстоянию между точками приложения реакций; при длинных опорах (обеспечивающих заделку концов балок) - расстоянию между гранями опор;
l - полная длина однопролетной рандбалки;
b - толщина стены; Я-высота стены над рандбалкой;
Eк - модуль упругости кладки стены, определяемый для расчетов по предельному состоянию; для неармированной кладки Ек = 0,5Е0 = 0,5 αRн, где α и Rн - соответственно упругая характеристика и нормативное сопротивление сжатию, принимаемые по нормам проектирования каменных конструкций;
Е - нормативный модуль упругости материала балки;
EI - жесткость рандбалки (для железобетонных рандбалок прямоугольного сечения Е = 12B/bh3, где В - жесткость, определенная с учетом арматуры по СНиП II-В. I-61).
Сосредоточенная нагрузка, приложенная к стене на высоте Н от верха рандбалки, может быть заменена нагрузкой, равномерно распределенной по длине пролета: для жесткой рандбалки при Н≥L для гибкой - при Н≥0,5 L.
Несколько сосредоточенных нагрузок (три и более) могут быть заменены равномерно распределенной нагрузкой: для жесткой рандбалки при H≥0,5 L; для гибкой - при H≥0,25 L.
Рандбалки рассматриваются как жесткие при показателе относительной гибкости K>0,1, который определяется по формуле:
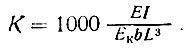
(II-1)
Замену сосредоточенных нагрузок равномерно распределенной следует производить и в том случае, когда они приложены над опорой рандбалки. Если расстояние от верха рандбалки до точки приложения сосредоточенной нагрузки меньше указанных выше, то распределение давления в кладке принимается под углом 45° к горизонту. Эпюры давлений, приходящиеся на единицу длины глухого участка стены в различных уровнях, приведены на рис. II-52, а.
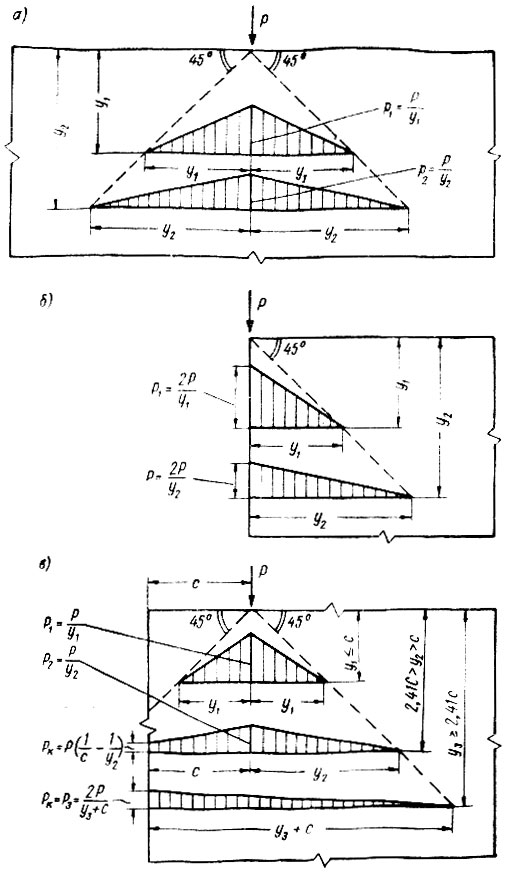
Рис. II-52. Распределение давления в кладке от сосредоточенной нагрузки. а - на глухом участке стены; б - у края стены; в - на некотором расстоянии от края стены
Наибольшая ордината эпюры давлений, соответствующая высоте треугольника и находящаяся на одной вертикали с точкой приложения нагрузки, определяется из условия равенства площади эпюры давления внешней сосредоточенной силе. Эпюра напряжений в рассматриваемом шве подобна эпюре давлений. Величина напряжения равна давлению на единицу длины стены, деленному на ее толщину, выраженную в тех же единицах меры длины, что и расстояние по вертикали от рассматриваемого шва до точки приложения сосредоточенной нагрузки. Например, при сосредоточенной (Нагрузке Р = 1000 кг, расстоянии от рассматриваемого шва до точки приложения нагрузки y = 100 см и толщине стены b = 25 см наибольшая ордината эпюры давлений
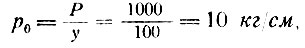
а наибольшая ордината эпюры напряжений
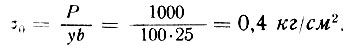
При расположении нагрузки у края стены, эпюра давлений принимает вид прямоугольного треугольника (рис. II-52, б). Если сосредоточенная нагрузка расположена на некотором удалении от края стены, эпюры давлений принимают очертания, приведенные на рис. II-52, в. Эпюры распределения давления в кладке от местной равномерной нагрузки, приложенной по верху стены, приведены на рис. II-53.
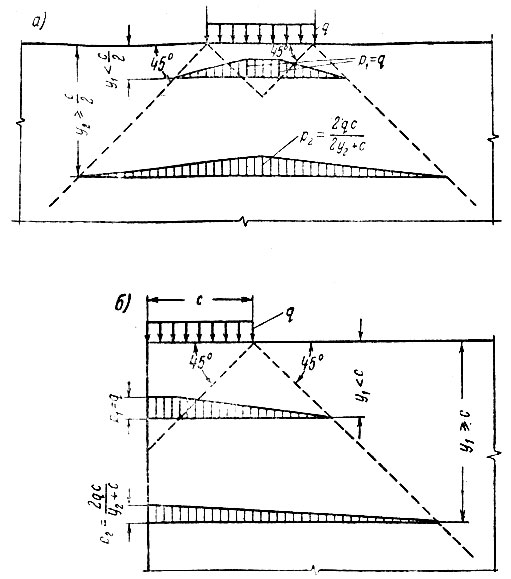
Рис. II-53. Распределение давления в кладке от равномерно распределенной нагрузки на ограниченном участке глухой стены. а - на среднем участке стены; б - у края стены
Формулы Б. Н. Жемочкина [10] для определения эпюр нагрузок на равдбалку применяются в зависимости от ее гибкости, определяемой по (II-1). В первом расчетном случае (затвердевшая кладка) при высоте стены, превышающей половину пролета для жесткой рандбалки или четверть пролета для гибкой, и при узких опорах эпюру нагрузок на рандбалку можно принять состоящей из треугольников (рис. II-54,а). Наибольшая ордината эпюры над опорой для этого случая
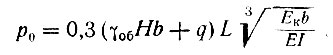
(II-2)
а длины полуоснований эпюр
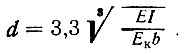
(II-3)
Если длины полуоснований эпюр превышают половину пролета рандбалки, то эпюры для смежных опор взаимно накладываются (рис. II-54, б). Если же длины полуоснований эпюр превышают пролет, что возможно при очень жестких рандбалках, то нагрузка принимается равномерно распределенной по длине рандбалки. Формулы (II-2) и (II-3) получены для промежуточных опор неразрезной рандбалки, но практически могут применяться и для крайней опоры с несколько большими ординатами, чем по формуле (II-2), а полуоснование - несколько меньше, чем по (II-3). Для затвердевшей кладки при достаточно высокой стене и при широких опорах эпюры нагрузки как для многопролетных, так и для однопролетных рандбалок можно принимать в виде треугольников (рис. II-54, б, г). Для обоих случаев наибольшая ордината эпюры (над краем простенка)
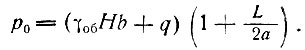
(II-4)
Длина основания каждого треугольника определяется по той же формуле (Н-3), что и в случае рандбалки на узких опорах, но она откладывается в данном случае не от оси опоры, а от ее края. В зависимости от условий заделки опор наклонные линии эпюр можно продолжить до принятого опорного сечения (при неглубоких заделках однопролетных рандбалок - до середины опоры), как показано пунктиром на рис. II-54,г; ордината над центром опоры вычисляется из подобия треугольников.
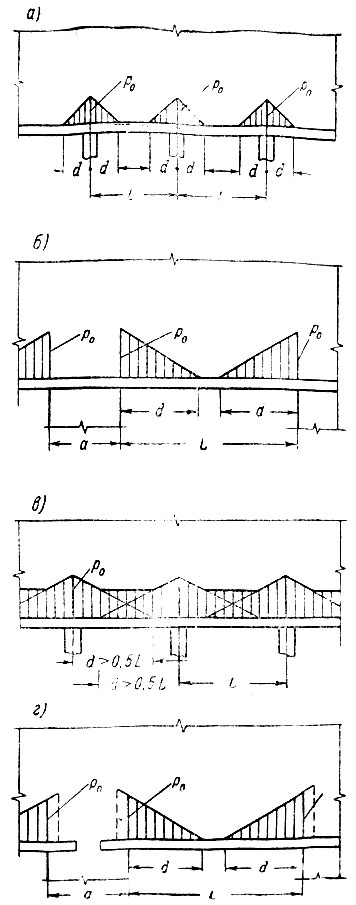
Рис. II-54. Эпюры нагрузки на рандбалку. а - при узких опорах и высоте стены более 0.5L для жесткой или 0.25 L - для гибкой; б - то же, при широких опорах; в - то же, что и а, но при d>0.5L; г - то же, что и а, но для однопролетнои рандбалки на широких опорах
Формулы (II-4) и (II-3) определяют ординаты над краем простенка и длины эпюр, когда опора под рандбалкой выполнена из того же материала и той же толщины, что и стена, которую она поддерживает. С возрастанием жесткости опоры за счет ее утолщения, уменьшения ее высоты или увеличения Ек значения Р0 и d возрастают; при абсолютно жестких опорах эти величины определяются по формулам (II-4) и (II-3) с коэффициентом 1,3.
Наибольшее краевое давление, вызывающее местное смятие кладки в крайних волокнах широкой опоры под неразрезной рандбалкой или под заделанными концами однопролетной балки (рис. II-55).
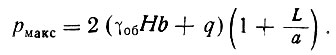
(II-5)
В случаях, когда опоры рандбалок не широкие, но и не достаточно узкие, для того, чтобы реакции опор можно было принять сосредоточенными, наибольшую ординату следует вычислить дважды, т. е. по формулам (II-2), (II-4), и принять меньшее значение. Длина эпюры d, вычисленная по формуле (II-3), при любом из принятых значений наибольшей ординаты p0 откладывается от края опоры.
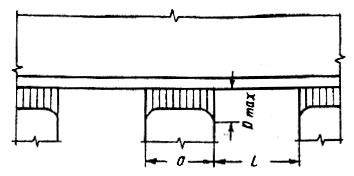
Рис. II-55. Краевое давление неразрезной балки на широкую опору
При незначительной высоте стены Н, не удовлетворяющей условиям H≥0,5L для жесткой рандбалки или H≥0,25 L для гибкой, вне зависимости от степени затвердевания кладки и ширины опор, нагрузку на рандбалку от внешней равномерно распределенной нагрузки на стену и от веса кладки стены следует считать также равномерно распределенной по длине рандбалки. Влияние сосредоточенных нагрузок учитывается отдельно.
Если рандбалка нагружена высокой стеной из свежеуложенной или оттаявшей после замораживания кладки, что соответствует второму расчетному случаю нагрузок, то рекомендуется:
- нагрузку от веса кладки до высоты H = 0,5 L для жесткой рандбалки или до высоты H = 0,25 L для гибкой считать равномерно распределенной (по прямоугольной эпюре) так же, как для стен незначительной высоты;
- нагрузку от вышележащей кладки и приложенных к ней внешних распределенных нагрузок в зависимости от ширины опор определять, пользуясь формулами (II-2) и (II-3) или (II-4) и (II-3) для первого расчетного положения;
- нагрузки от сосредоточенных сил принять по эпюрам распределения давления в кладке;
- статический расчет рандбалок производить по суммарной эпюре нагрузок или суммарным изгибающему моменту, поперечной силе и прогибу, вычисленным для каждого вид нагрузок, включая ее собственный вес.
При определении эпюры наугрузок можно не учитывать оконные и дверные проемы, если последние расположены IB середине пролета и ширина их не превышает 20% от длины пролета рандбалок.
Если низ больших проемов находится от верха рандбалки на высоте, превышающей длину пролета при жестких рандбалках или половину длины пролета при гибких, то всю нагрузку на уровне низа проемов можно заменить равномерно распределенной и эпюры нагрузки на рандбалку определять по формулам (II-2) и (II-3) или (II-4) и (II-3), в зависимости от ширины опор. При больших проемах, расположенных ниже, чем указано, нагрузку на уровне их низа следует считать равномерно распределенной в пределах ширин простенков: нагрузка на рандбалку в этом случае определяется с учетом распределения давления в кладке. Величиной С в данном случае явится ширина простенка (рис. II-53, а).
При наличии проема для ворот в средней части пролета рандбалки на узких опорах эпюры нагрузок следует принимать треугольными (рис. II-56, г) Наибольшая ордината
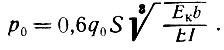
(II-6)
В формуле (II-2) средняя интенсивность нагрузки γобHb + q считается распространенной по всему пролету и в связи с этим множится на L. В формуле (II-6) средняя интенсивность нагрузки q0 = (γобHb + q)L/2S множится на ширину простенка 2S. Половина длины эпюры d определяется по формуле (II-3).
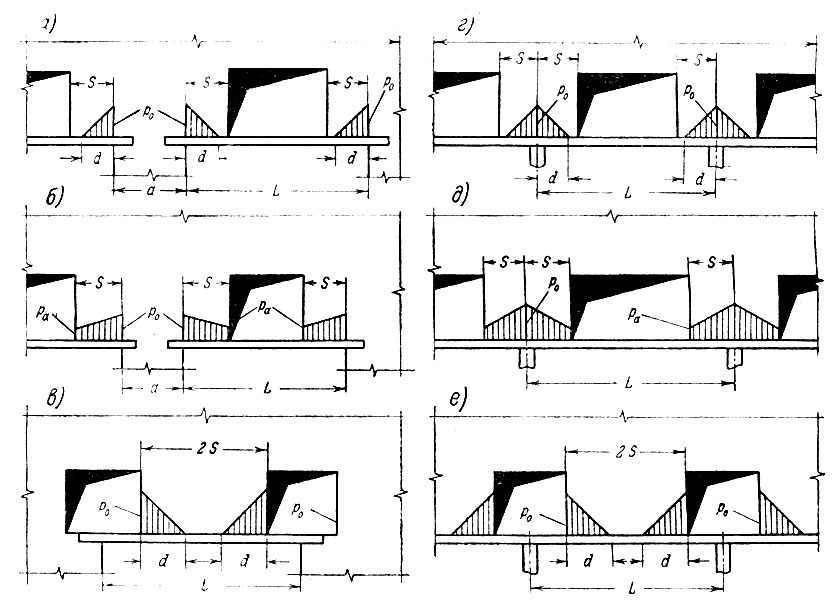
Рис. II-56. Эпюры нагрузки на рандбалку от кладки с проемами. а - при широких опорах и d<S; б - то же, при d>S; в - при проемах над широкими опорами; г - при узких опорах и d>S; д - то же, при d>S; е - при проемах над узкими опорами
В тех случаях, когда при наличии проема в средней части пролета длина эпюры, равная 2d, превышает ширину простенка 2S, эпюру следует принимать в виде трапеции (рис. II-56, д). Ордината над центром опоры P0 определяется по-прежнему по формулам (II-2) или (II-6). Ордината у края отверстия
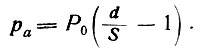
(II-7)
Если pa≥p0, то нагрузку на рандбалку под простенком следует принимать равномерно распределенной. Проем для ворот в средней части пролета рандбалки, лежащей на широких опорах, следует учитывать лишь при d>S; эпюра нагрузок при d<S показана на рис. II-56, а.
Наибольшую ординату эпюры (над краем опоры) можно определить по формуле (II-4), при интенсивности нагрузки, равной γобHb + q,- по всей длине стены. Применив интенсивность нагрузки в пределах простенка (т. е. по ширине, равной a + 2S) 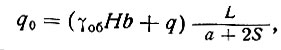 наибольшую ординату можно определить по формуле:
наибольшую ординату можно определить по формуле:
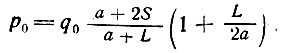
(II-8)
Длина эпюры d, как и ранее, определяется по формуле (II-3).
Для случая, когда d>S, эпюры (рис. II-56, б) принимают форму трапеций и ординаты у проема, как и в случае с узкими опорами, определяются по формуле (II-7), Если ордината эпюры у проема ра окажется большей или равной ординате над краем опоры р0, нагрузку следует принимать равномерно распределенной.
Когда проемы расположены над опорами (рис. II-56, в, е), то вне зависимости от ширины последних эпюры нагрузки на рандбалку от простенков также можно считать треугольными. Наибольшая ордината эпюры (у края проема)
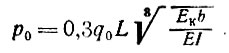
(II-9)
В отличие от формулы (II-2) в формуле (II-9) средняя интенсивность нагрузки, обозначенная через q0, должна быть подсчитана в пределах простенка между проемами шириной 2S. Длина основания каждого треугольника
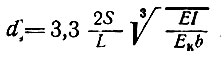
(II-10)
Если d>S, эпюры в средней части рандбалки суммируются; если же d>2S, то нагрузку на рандбалку под простенком между проемами следует считать равномерно распределенной
В методе М. Я. Пильдиша и С. В. Полякова [12] рандбалка высотой h условно заменяется слоем кладки толщиной h0, эквивалентным по способности распределения реакций опор, т. е равным по жесткости. В этом случае вычисляются ординаты эпюры давления на глубине h0, соответствующие ординатам эпюры давления в плоскости шва между кладкой и реальной рандбалкой.
На рис. II-57 приведена примерная схема расчета рандбалки с условной эпюрой давления.
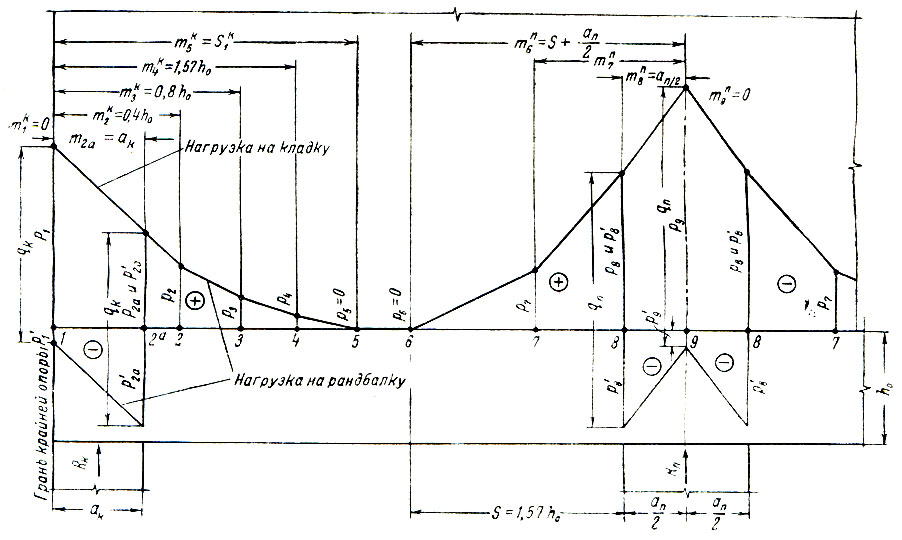
Рис. II-57. Схема эпюр нагрузок к расчету рандбалки и кладки
В пролете рандбалки эпюра давления на кладку является в то же время и эпюрой нагрузки на рандбалку; ординаты эпюры в пролете принимаются положительными. В пределах опор ординаты эпюры нагрузки на рандбалку определяются как разность между значением ординат давления на кладку и интенсивностью давления опор. Ординаты эпюры нагрузки на рандбалку в пределах опор имеют отрицательные значения (рис. II-57).
Эпюра нагрузки принимается состоящей из отрезков прямых, соединяющих вычисленные и отложенные в масштабе ординаты для характерных точек, обозначенных на рисунке цифрами без индекса а. Количество характерных точек сведено к минимуму и состоит из пяти в зоне крайней опоры и четырех - в зоне промежуточной опоры. Привязки характерных точек 1, 2, 3, 4, 5, 6 и 9 не зависят от ширины опоры. Для точек 7 и 8 привязки изменяются в зависимости от ширины промежуточной опоры и в связи с этим их значения приводятся для каждого конкретного случая. Ординаты для промежуточных точек у внутренней грани крайней опоры, обозначенных на рис. II-57 через 2а соответственно в других случаях в зависимости от ширины крайней опоры -3а, 4a или 5а - определяются путем интерполяции.
Расчет рандбалки по рассматриваемому методу сводится к вычислению следующих величин:
- ординат эпюры давления на кладку;
- наибольших напряжений в кладке над опорами рандбалок (для проверки прочности кладки);
- ординат эпюры нагрузки на рандбалку, поперечных сил и изгибающих моментов.
При этом ординаты эпюры поперечных сил определяются в результате вычисления и последовательного суммирования элементарных площадей эпюры нагрузки на рандбалку, а ординаты эпюры изгибающих моментов -в результате вычисления и последовательного суммирования элементарных площадей эпюры поперечных сил.
Исходными данными для вычисления ординат эпюры давления на кладку в характерных точках (рис. II-57) являются:
Rк - реакция крайней опоры рассчитываемой рандбалки в т;
Rп -то же, промежуточной опоры;
ак - ширина крайней опоры рандбалки, обусловленная размерами сечения стойки-фундамента в м;
ап - то же, промежуточной опоры;
qк = Rк/ак - погонная нагрузка от стойки-фундамента на рандбалку (снизу) в пределах крайней опоры в т/м;
qп = Rп/ап - то же, в пределах промежуточной опоры;
b - толщина стены в м;
h - высота рандбалки в м;
E - нормативный модуль упругости материала рандбалки в кг/см2 или т/м2;
I - момент инерции рандбалки в м4;
Eк = 0,5αRн - модуль упругости кладки, где α и Rн - соответственно ее упругая характеристика и нормативное сопротивление сжатию, отвечающие расчетному случаю нагрузок;
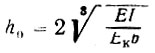
- приведенная высота рандбалки в м; для прямоугольного сечения проще воспользоваться формулой 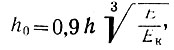 где h - высота сечения;
где h - высота сечения;
ак/h0 - отношение ширины крайней опоры к приведенной высоте рандбалки, являющееся критерием при выборе формул для вычисления ординат эпюры давления на кладку в зоне крайней опоры (с p1 по p5);
Sк1 - длина эпюры давления на кладку в зоне крайней опоры (от наружной грани опоры до нулевой точки 5), принимаемая по табл. II-9 в зависимости от отношения ак/h0.

Таблица II-9. Длина эпюры Sк1 в долях h0
S = 1,57h0 - радиус действия реакции промежуточной опоры в м, равный расстоянию от нулевой точки 6 эпюры давления на кладку в зоне промежуточной опоры до ближайшей к ней грани опоры;
Sк1 = 2S + ап - длина эпюры давления в зоне промежуточной опоры в м;
ап/S - отношение ширины промежуточной опоры к радиусу действия реакции опоры, являющееся критерием при выборе формул для вычисления ординат эпюры давления на кладку в зоне промежуточной опоры (с p6 по p9).
Формулы, определяющие значения ординат эпюры нагрузок в каждой характерной точке, различны для разных соотношений ак/h0 в зоне крайней опоры и ап/S - в зоне промежуточной опоры.
Общее количество возможных расчетных случаев, зависящих от этих соотношений, исчерпывается следующими:
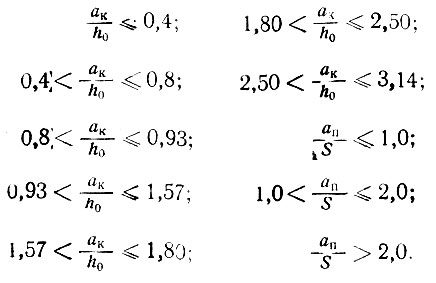
Первые семь неравенств относятся к зоне крайней эпюры, последние три - к промежуточной.
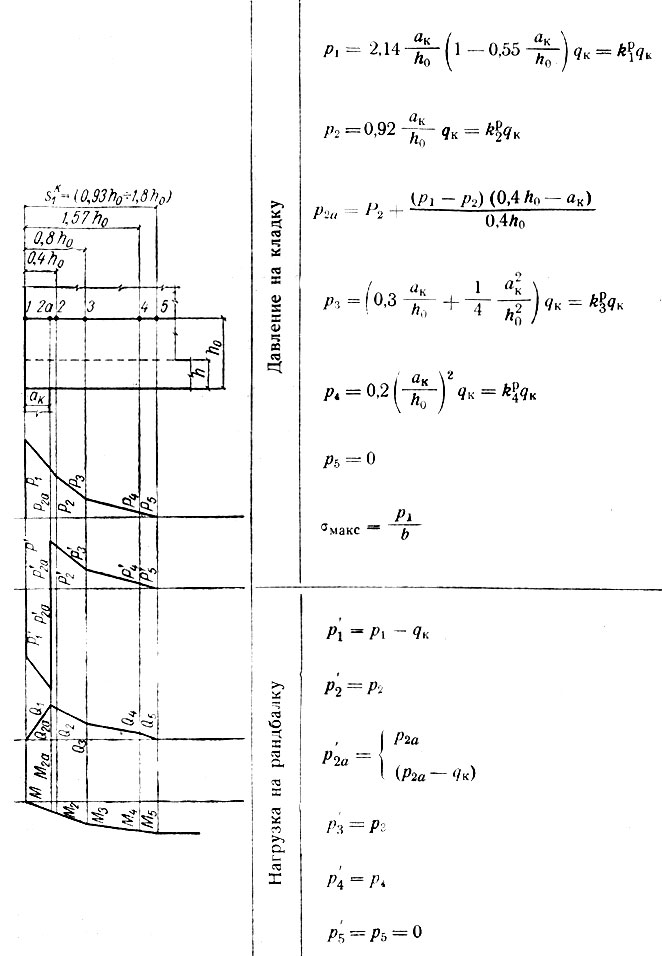
Таблица II-10. Расчет крайней опоры при ак/h0<0,4
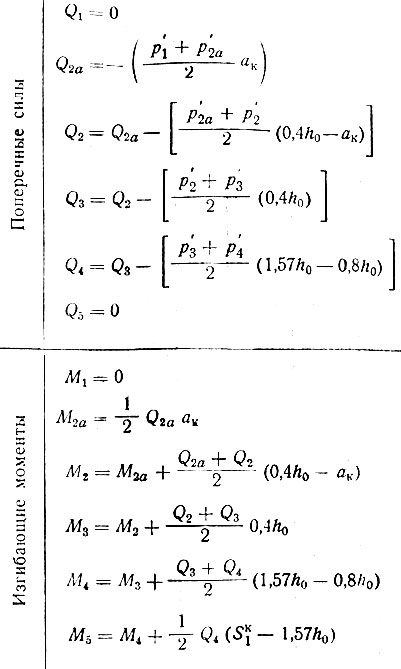
Таблица II-10. Продолжение
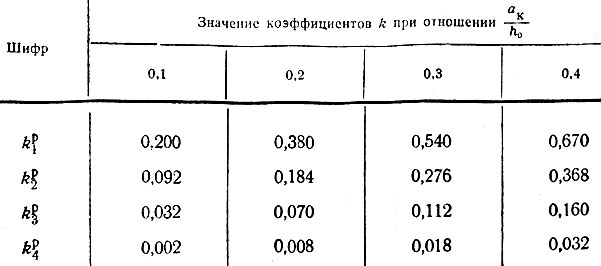
Таблица II-10. Продолжение
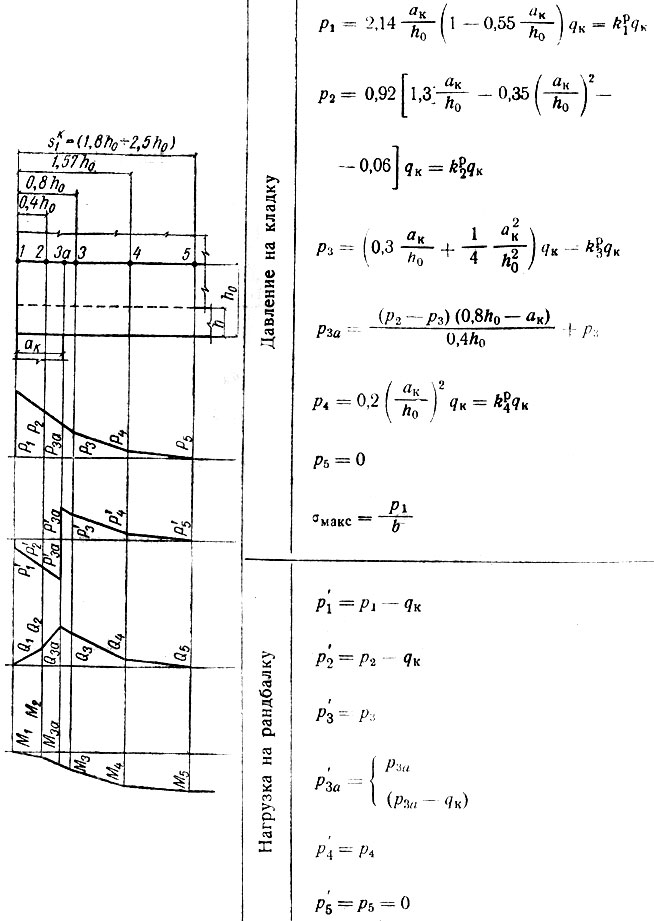
Таблица II-11. Расчет крайней опоры при 0,4<ак/h0<0,8
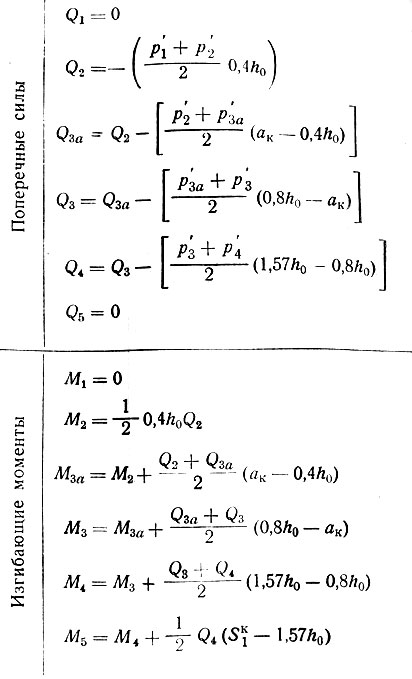
Таблица II-11. Продолжение
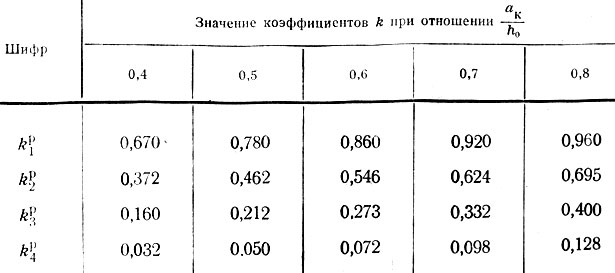
Таблица II-11. Продолжение
Для каждого из перечисленных случаев составлены отдельные расчетные таблицы (с II-10 и по II-19), в которых приведены все формулы, необходимые для вычисления ординат эпюр давления на кладку стены р, нагрузки на рандбалку р' поперечных Q и изгибающих моментов М; представлены схемы опорных зон рандбалок и указаны характерные точки, примерные формы эпюр, а также числовые значения множителей, входящих в формулы и допускающих предварительное их вычисление. Эти множители (коэффициенты) обозначены во втором написании формул литерой К с двумя индексами: нижний, числовой, указывает характерную точку эпюры, а верхний, буквенный, к какой эпюре относится вычисляемая ордината (р, Q или М).
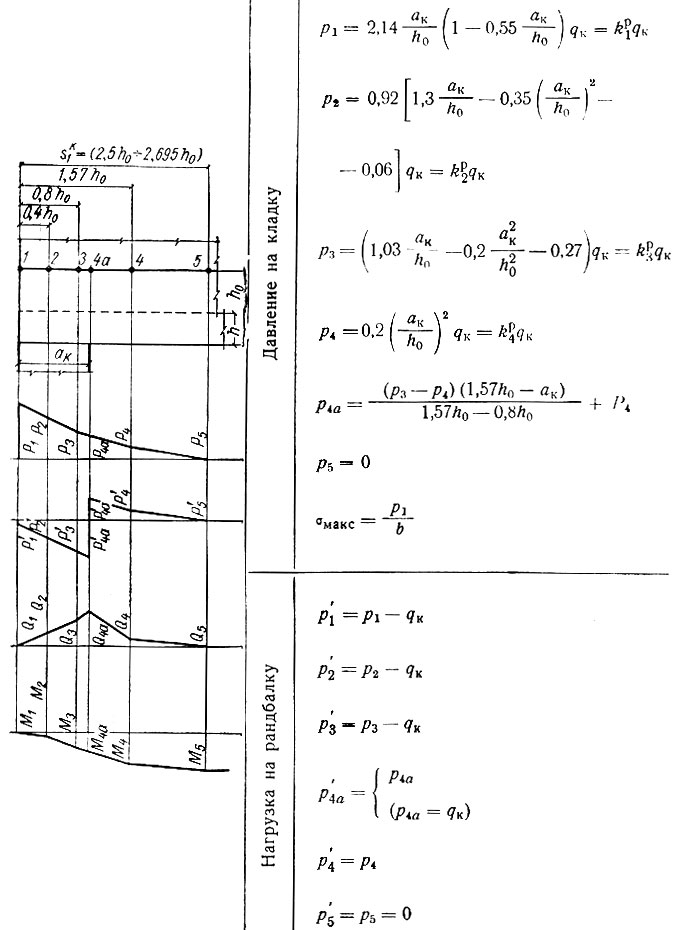
Таблица II-12. Расчет крайней опоры при 0,8<ак/h0<0,93
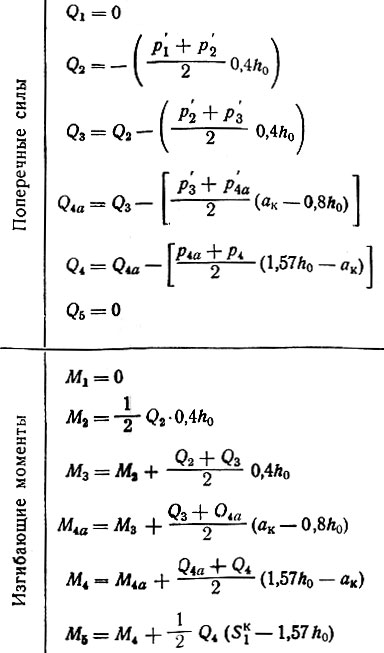
Таблица II-12. Продолжение
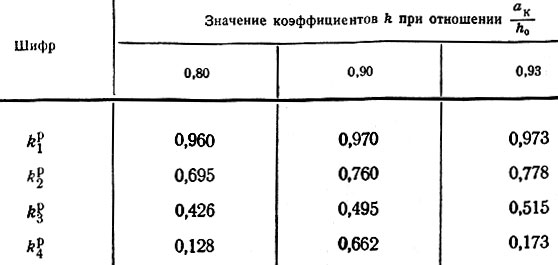
Таблица II-12. Продолжение
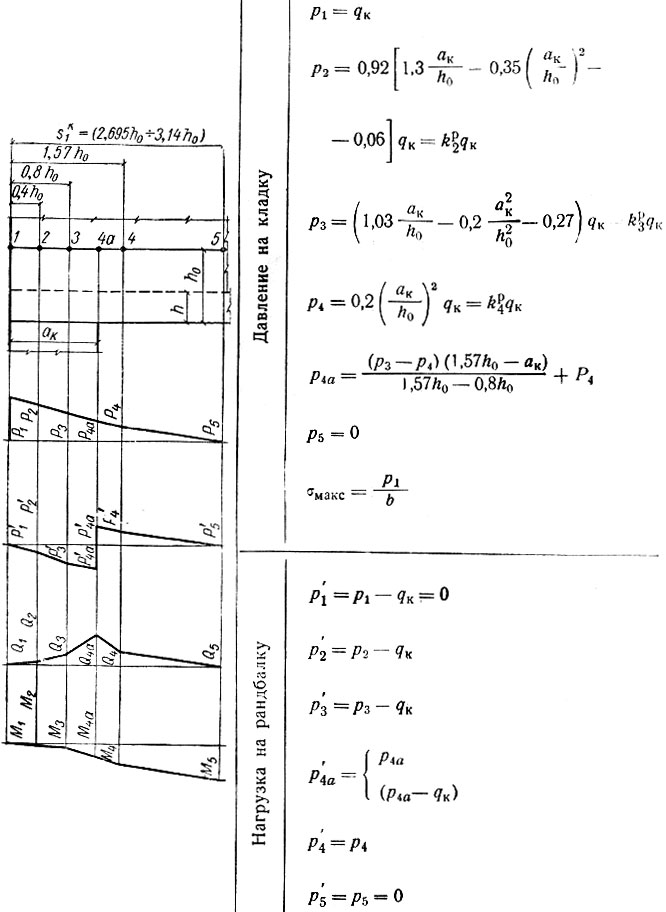
Таблица II-13. Расчет крайней опоры при 0,93<ак/h0<1,57

Таблица II-13. Продолжение
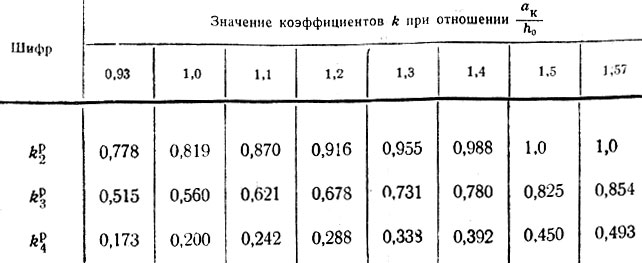
Таблица II-13. Продолжение
Для приближенного статического расчета неразрезной рандбалки под стену без проема необходимо:
- определить исходные данные, соответствующие расчетным случаям нагрузки;
- по величинам ак/h0 и ап/S подобрать соответствующие расчетные таблицы;
- по приведенным в таблицах формулам определить ординаты эпюр давления на кладку, нагрузки на рандбалку, ординаты поперечных сил и изгибающих моментов, а также максимальное напряжение в кладке.
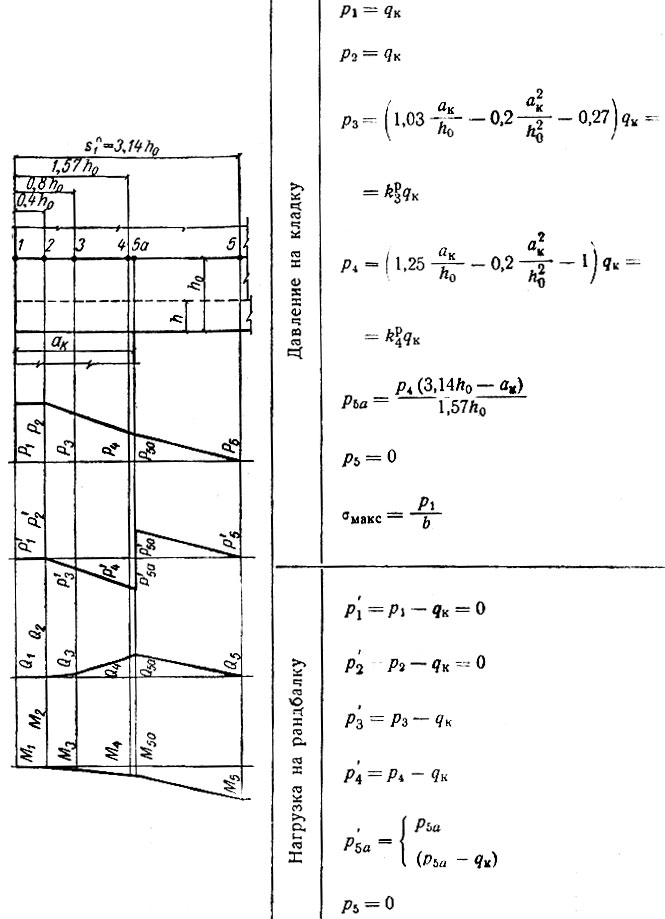
Таблица II-14. Расчет крайней опоры при 1,57<ак/h0<1,8
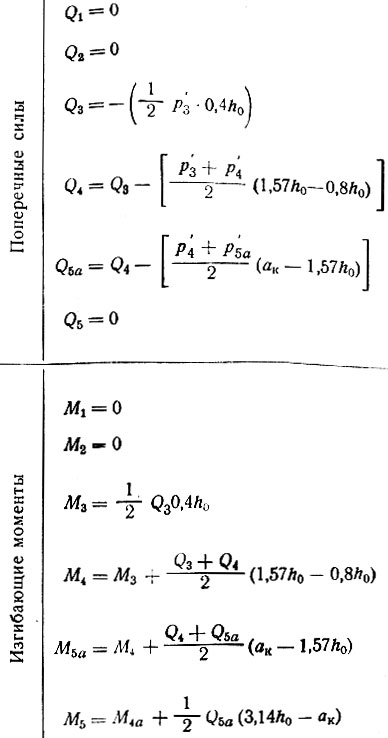
Таблица II-14. Продолжение
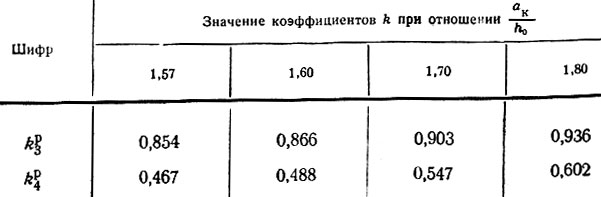
Таблица II-14. Продолжение
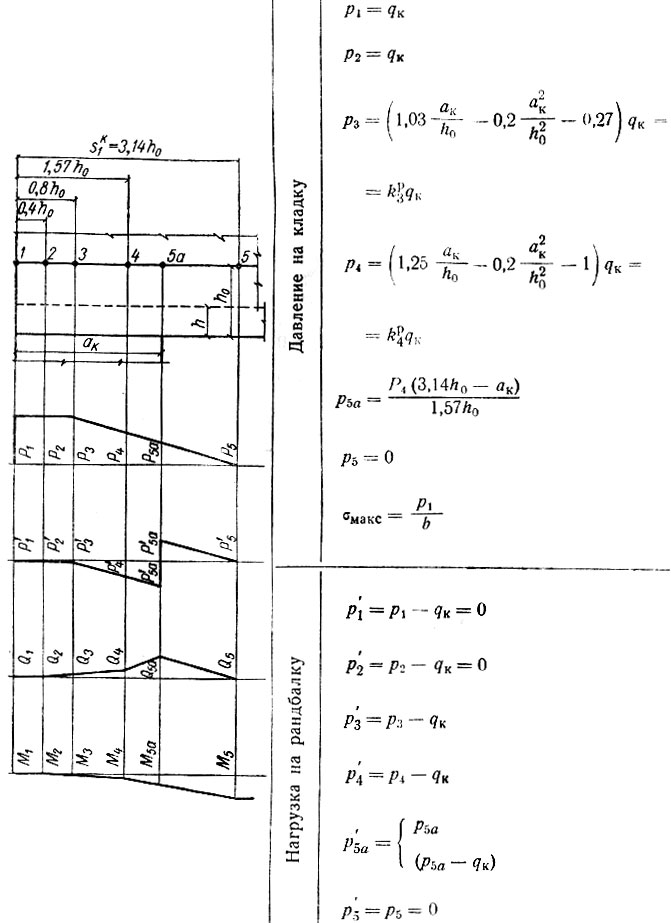
Таблица II-15. Расчет крайней опоры при 1,80<ак/h0<2,50
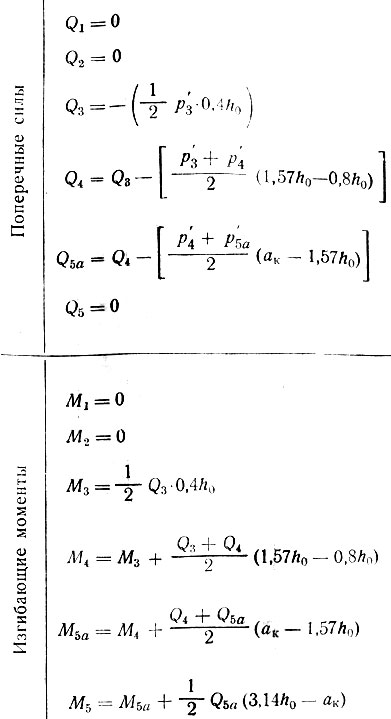
Таблица II-15. Продолжение
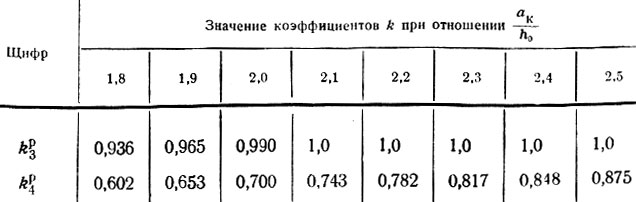
Таблица II-15. Продолжение
При жестких рандбалках или при слабой кладке эпюры нагрузки на рандбалку для зон крайней и промежуточной опор могут взаимно накладываться в средней части пролета. В месте наложения эпюр Р1 следует ординаты суммировать, проведя линию, ограничивающую суммарную эпюру P1. Ординаты эпюры Q вычисляют последовательным суммированием (алгебраическим) элементарных площадок, заключенных между смежными ординатами в характерных точках суммарной эпюры Р1. Ординаты эпюры М вычисляются последовательным суммированием таких же площадок эпюры Q.
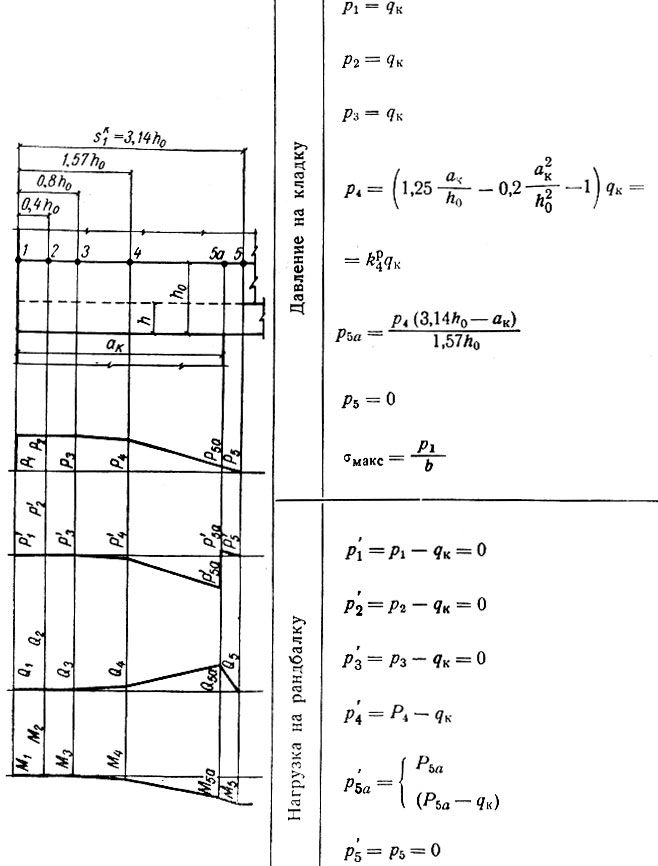
Таблица II-16. Расчет крайней опоры при 2,50<ак/h0<3,14
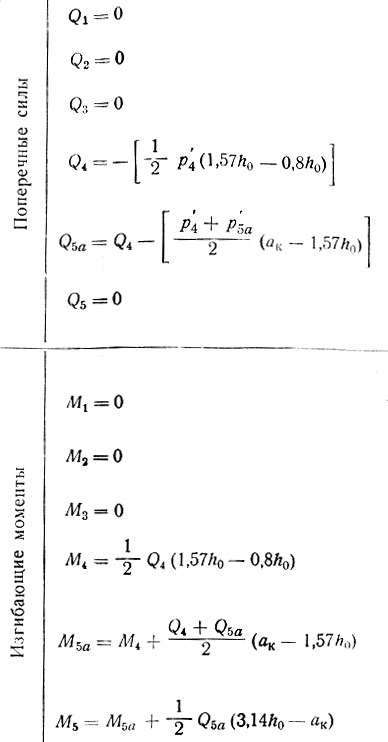
Таблица II-16. Продолжение
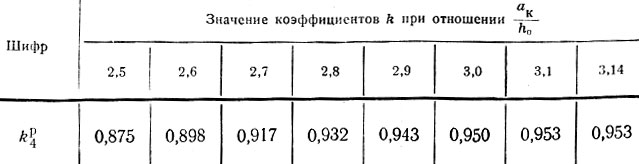
Таблица II-16. Продолжение
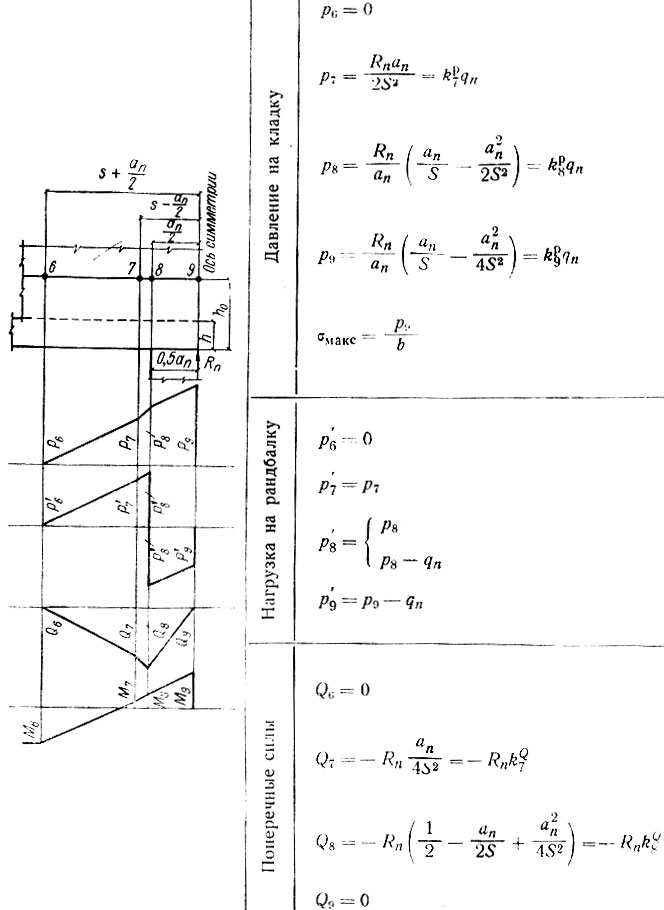
Таблица II-17. Расчет промежуточной опоры при ап/S<1,0

Таблица II-17. Продолжение
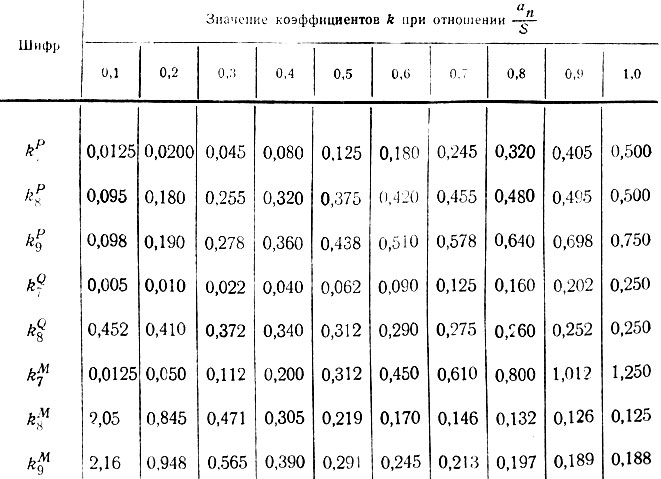
Таблица II-17. Продолжение
М. Я. Пильдиш и С. В. Поляков рекомендуют не учитывать влияние одного проема на работу рандбалки; при нескольких проемах в одном пролете, а также при расположении проема над опорой этот метод не применим.
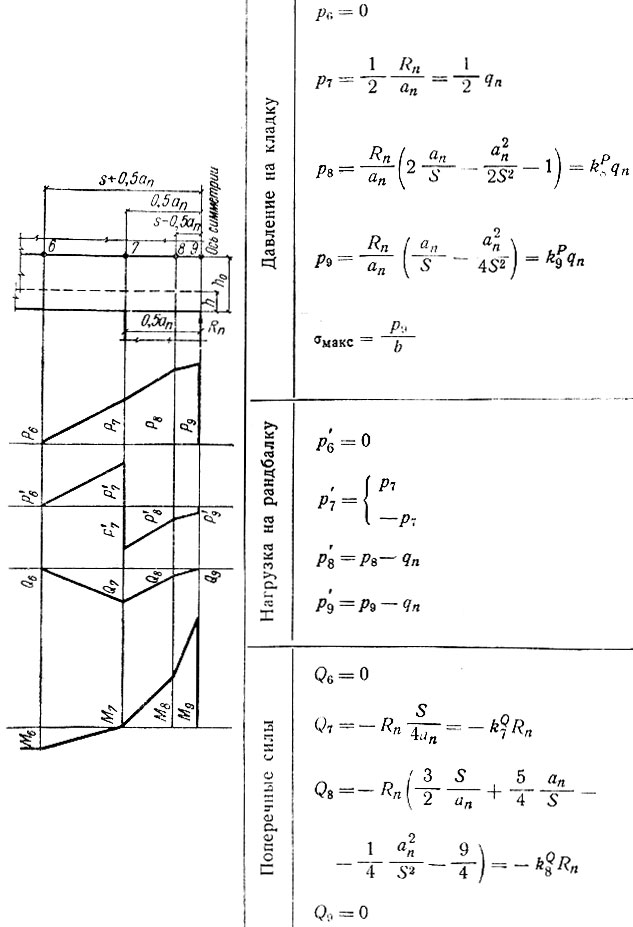
Таблица II-18. Расчет промежуточной опоры при 1<ап/S<2

Таблица II-18. Продолжение
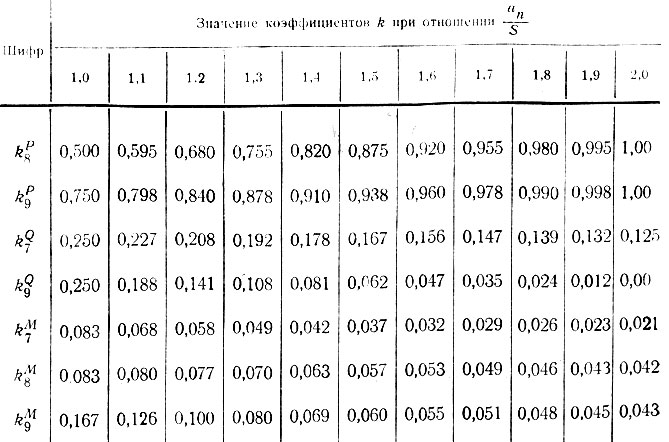
Таблица II-18. Продолжение
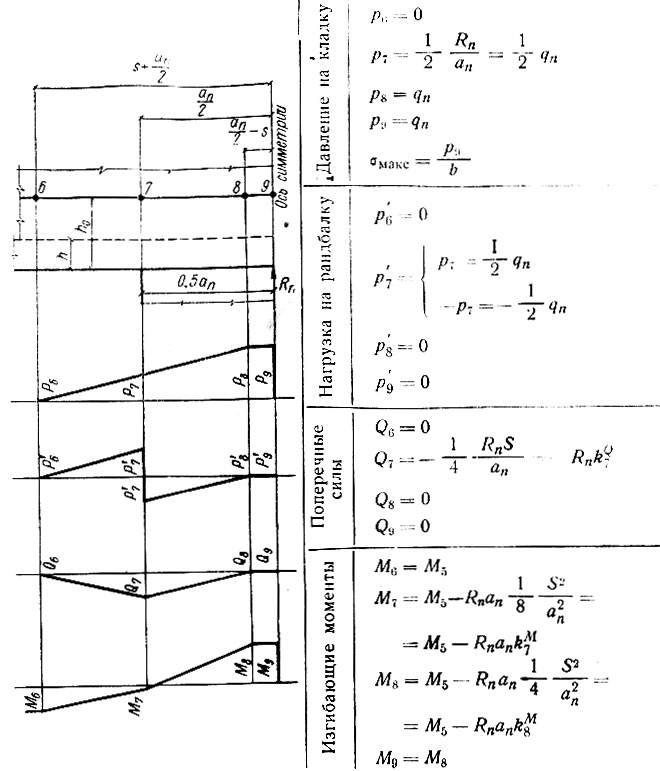
Таблица II-19. Расчет промежуточной опоры при ап/S>2
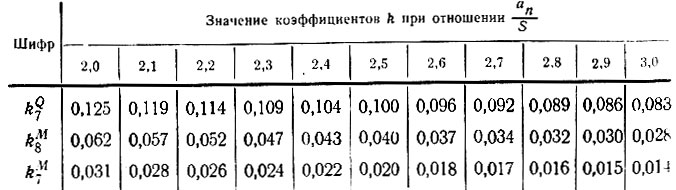
Таблица II-19. Продолжение
Влияние проема на работу кладки стены учитывается в случае, если ширина простенка над крайней опорой Cк≤0,93 h0 и над промежуточной опорой Cп≤3,14 h0. В этих случаях максимальные ординаты эпюры давления на кладку стены без проема принимаются с коэффициентами:
- над промежуточной опорой:
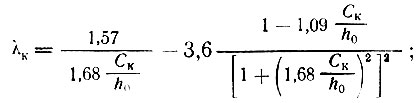
(II-11) - над промежуточной опорой:
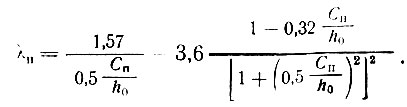
(II-12)
Числовые значения коэффициентов λк и λп в зависимости от Ск/h0 и Сп/h0 приведены в табл. II-20 и II-21.
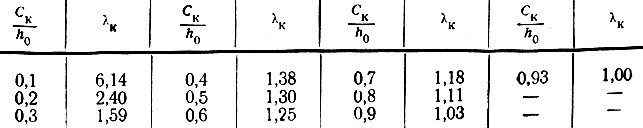
Таблица II-20. Значения λк
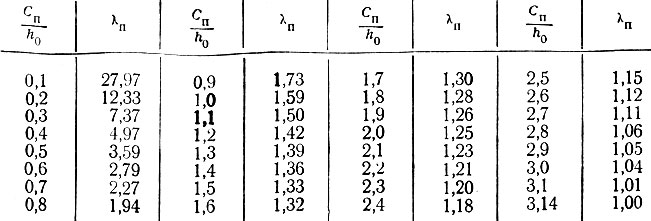
Таблица II-21. Значения λп
В формулах П. А. Гагарина для изгибающих моментов имеется показатель относительной гибкости рандбалок
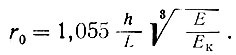
(II-13)
Однопролетная рандбалка считается гибкой, если r0<0,5 и жесткой при rв≥0,5.
Максимальный изгибающий момент в пролете свободно лежащей однопролетной рандбалки
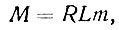
(II-14)
где m - безразмерный коэффициент, зависящий от ее гибкости (табл. II-22).
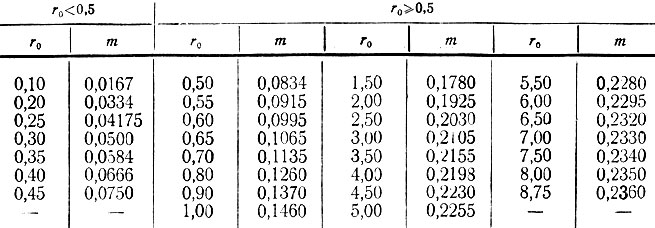
Таблица II-22. Безразмерные коэффициенты m
Для гибких рандбалок
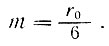
(II-15)
Для жестких рандбалок
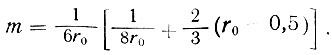
(II-16)
Максимальная поперечная сила (в сечении над точкой приложения опорной реакции)*
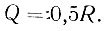
(II-17)
* (Промстройпроект предлагает поперечную силу принимать с коэффициентом запаса прочности 1,6.)
В случае частичного защемления опор максимальный момент в пролете балки
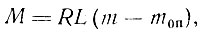
(II-18)
где mоп - безразмерный коэффициент, определяемый вне зависимости от степени относительной гибкости рандбалки.
Этот коэффициент
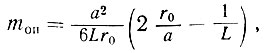
(II-19)
где а - расстояние от точки приложения опорной реакции до конца балки.
Пример. Определить усилия в сборной железобетонной рандбалке длиной 6 м. Нагрузка - собственный вес кирпичной стены высотой 4 м, толщиной 51 см; кирпич марки 75 на растворе марки 25; бетон рандбалки марки 150. Длина опирания концов рандбалки равна 22,5 см. Полагая, что точка приложения опорной реакции находится на расстоянии 22,5/3 = 7,5 см от внутренней грани опоры, расчетный пролет L = 6,0-0,15*2 = 5,7 м. Сечение ориентировочно принято 52×45 см.
Величина опорной реакции с коэффициентом перегрузки 1,1
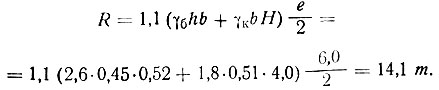
Модуль упругости кладки по нормам проектирования каменных конструкций Eк = 0,5×750×22 = 8250 кг/см2.
Нормативный модуль упругости бетона М-150 по нормам проектирования железобетонных конструкций E = 240 000 кг/см2.
По формулам (II-13)-(II-17)
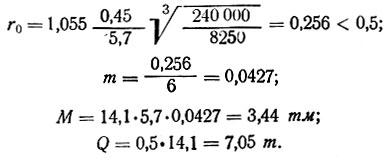
В случае защемления на опоре из значения изгибающего момента в пролете следует вычесть величину опорного момента
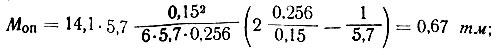
тогда
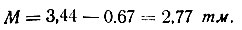
По полученным значениям изгибающих моментов и поперечных сил следует проверить сечение рандбалки и подобрать арматуру, если кладка не подвергалась замораживанию.
Если кладка производилась методом замораживания и к моменту первого оттаивания раствор имеет прочность, соответствующую марке 2, то
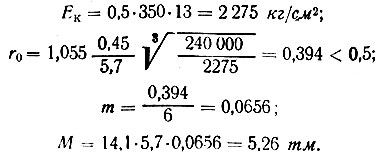
Как видно из сравнения полученных результатов, с понижением жесткости кладки, изгибающие моменты в пролете возрастают; поэтому при проектировании рандбалок под кладку, возводимую методом замораживания, и ори пучинистых грунтах, исключающих применение временных стоек в пролете, решающее значение приобретает второй расчетный случай загрузки.
|
|
При копировании обязательна установка активной ссылки:
http://townevolution.ru/ 'История архитектуры и градостоительства'