§ 2. Расчет глубин протаивания и сезонного промерзания

Нормативная глубина сезонного промерзания у фундаментов наружных стен определяется по данным многолетних наблюдений или рассчитывается по упрощенной формуле В. С. Лукьянова [13]:

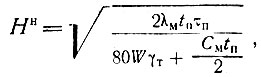
(III-52)

где λ_м - коэффициент теплопроводности в ^ккал/_{м×ч×град};

С_м - теплоемкость мерзлого грунта в ^ккал/_{м³×град};

γ_т - объемный вес скелета талого грунта, принимаемый по лабораторным данным в ^кг/_м³;

W - влажность в долях единицы без учета незамерзшей воды;

t_п - средняя температура воздуха в °С за время промерзания τ_п в ч; величины t_n и τ_п определяются по климатическим справочникам.

Расчетная глубина сезонного промерзания

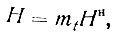
(III-53)

где m_t - коэффициент теплового влияния, принимаемый по действующим нормам.

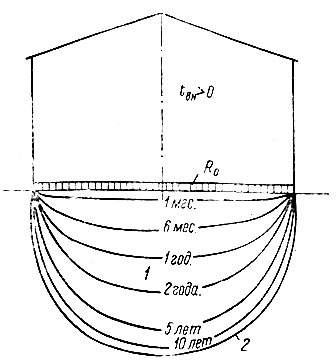
Рис. III-46. Образование чаши протаивания под отапливаемым зданием по М. Д. Головко. 1 - талый грунт; 2 - предельное очертание чаши протаивания

Развитие чаши протаивания под зданиями показано на рис. III-46 по расчетным данным в условиях однородной среды и на рис. III-47 по данным наблюдений [2].

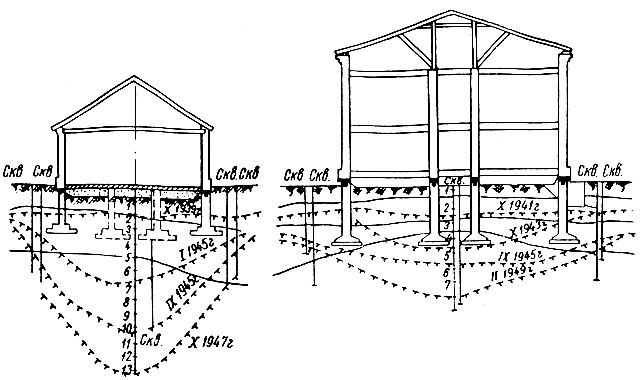
Рис. III-47. Протаивание оснований под отапливаемыми зданиями в г. Воркуте по данным наблюдений

Со временем теплообмен между зданием и грунтом приобретает стационарный характер, граница чаши протаивания достигает предельного значения и лишь вблизи наружных стен устанавливается периодический режим, обусловленный сезонными колебаниями температуры на поверхности.

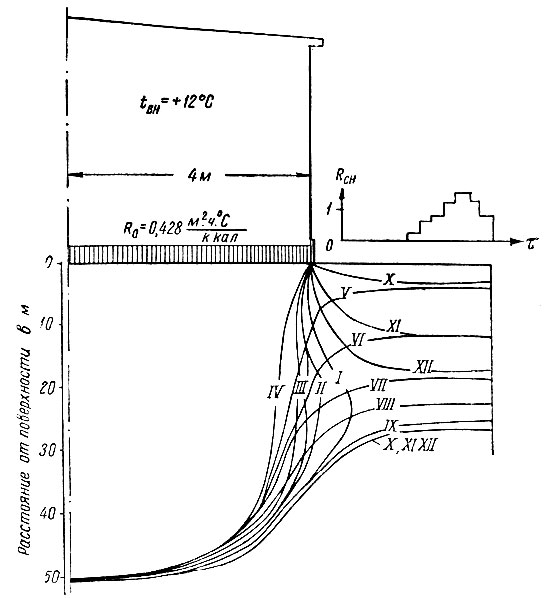
Рис. III-48. Колебание границы протаивания под краем здания в течение года по М. Д. Головко

Пример сезонных колебаний границы талых, грунтов у наружных стен здания показан на рис. III-48.

По данным Г. В. Порхаева [13], время τ, в течение которого чаша протаивания достигает предельного значения,зависит в первую очередь от температуры вечномерзлых грунтов у границы зоны нулевых годовых амплитуд (табл. III-32).

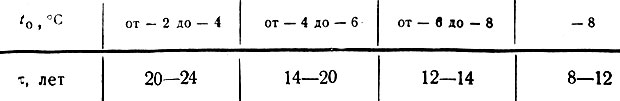
Таблица III-32. Ориентировочные данные о времени формирования чаши протаивания под зданием

Определение чаши протаивания под сооружениями в инженерной практике может производиться:

1. по формулам и номограммам М. Д. Головко, Г. В. Порхаева, С. В. Томирдиаро и В. П. Ушкалова (17; 13; 18; 14];
2. методами гидро- и электромоделиравания;
3. по методу конечных разностей [17].

Номограмма М. Д. Головко позволяет сравнительно просто получить максимальную глубину протаивания под зданием при симметричной двухмерной задаче.

Формула В. П. Ушкалова дает возможность рассчитать глубину протаивания за определенное время и, следовательно, определить начальную скорость протаивания под фундаментами.

Расчет Г. В. Порхаева более трудоемок, но позволяет определить не только максимальную глубину чаши протаивания, но и построить ее очертание.

Решение С. В. Томирдиаро дает возможность построить стационарное двухмерное температурное поле с учетом взаимного влияния нескольких сооружений.

Результаты расчета различными методами не совпадают - у С. В. Томирдиаро глубина протаивания получается несколько больше, чем у М. Д. Головко и несколько меньше, чем у Г. В. Порхаева.

Если пренебречь влиянием градиента температуры вечномерзлых грунтов (grad t), то решения М. Д. Головко для определения конечной глубины протаивания, а для расчета ее скорости методом В. П. Ушкалова.

Определение чаши протаивания с использованием гидравлических и электрических аналогий требует специального оборудования - интеграторов. Применение гидроинтеграторов необходимо при решении задач во времени, а электроинтеграторов для расчетов установившихся процессов. При этом сеточные электроинтеграторы рекомендуются в тех случаях, ковда необходимо учесть влияние на йротаивание неоднородности грунта, подземных телловыделяющих устройств (трубопроводов, кабелей), подземных резервуаров и др. В более прдстых случаях, например, для расчета протаивания под сооружениями на насыпях, следует применять электроинтеграторы с непрерывной средой.

Расчет методом конечных разностей очень трудоемок; для построения одного установившегося температурного поля требуется около месяца работы вычислителя.

При определении зоны оттаивания фильтрующих грунтов необходимо иметь в виду, что грунтовые воды могут существенно искажать форму и размеры чаши протаивания.

Метод расчета, предложенный М. Д. Головко, разработан на основе обобщения результатов, полученных путем построения чаш протаивания на электроинтеграторе, с непрерывной средой при граничных условиях (рис. III-49.).

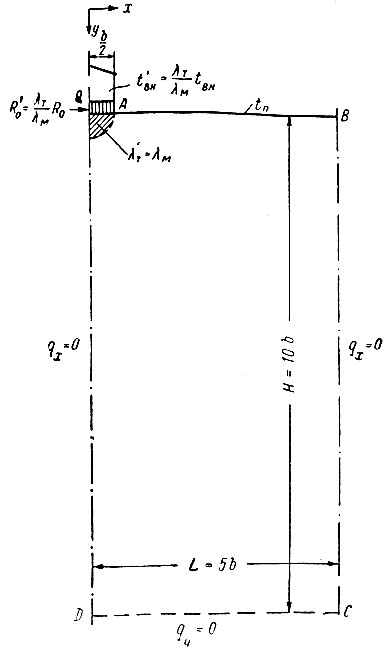
Рис. III-49. Граничные условия, принятые М. Д. Головко

Поэтому интеграторы с непрерывной средой, целесообразно применять в случаях более сложного, рельефа поверхности по сравнению с показанным на рис. III-49 или когда расчетные параметры выходят за пределы номограммы.

Расчет выполняется последовательно:

вычисляем параметр ^λ_тR₀/_В и коэффициент

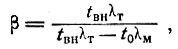
(III-54)

где λ_т и λ_м - теплопроводности грунта в талом и мерзлом состояниях в ^ккал/_{м×ч×град};

t_вн - температура воздуха помещения в °С;

В - ширина здания в м;

R₀ - термическое сопротивление пола, определяемое по СНиП, в ^{м2×ч×град}/_ккал.

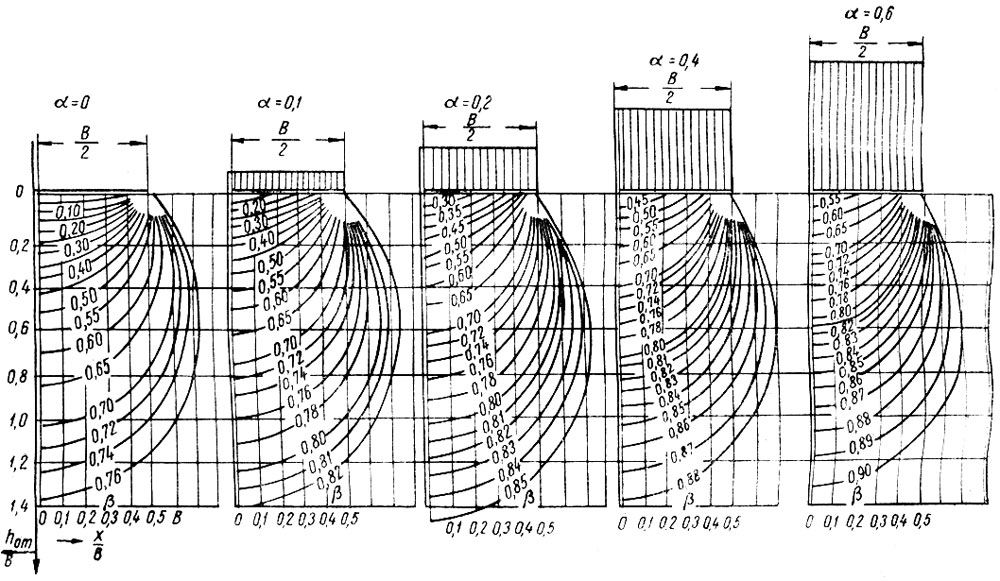
Рис. III-50. Графики М. Д. Головко для расчета глубины протаивания

На рис. III-50 по параметру ^λ_тR₀/_В выбирается необходимый для расчета график, а по величине β - кривая, определяющая границу протаивания; ординату этой кривой ^y/_B умножают на ширину здания В и получают глубину протаивания. В верхних слоях грунтов кривые условны, так как здесь граница протаивания колеблется в течение года под влиянием сезонных колебаний температур на поверхности.

Уравнение В. П. Ушкалова представляет собой решение одномерной задачи с эмпирическим поправочным коэффициентом k_τ перехода к трехмерной [14]; значения k_τ (рис. III-51) получены по материалам наблюдений за чашами протаивания значительного количества сооружений, дополненных результатами моделирования.

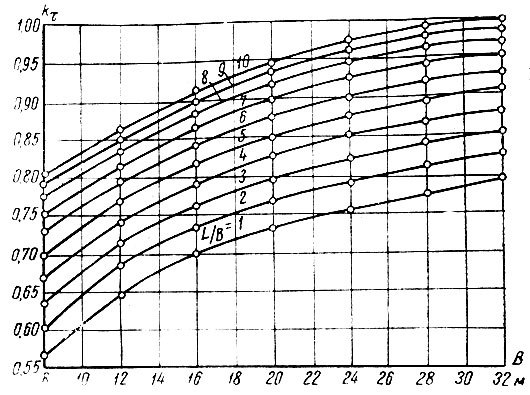
Рис. III-51. Графики kτ для расчета протаивания по В. П. Ушкалову

Глубина протаивания под серединой здания

(III-55)

где q - расход тепла на 1 м³ грунта, равный 80 (W - W_H)γ_м;

λ_т и λ_м - теплопроводности талых и мерзлых грунтов в ^ккал/_{м×ч×град};

С_т и С_м - объемные теплоемкости талых и мерзлых грунтов в ^ккал/_{мг×град};

τ - время в ч;

γ_м - объемный вес скелета мерзлого грунта естественного сложения в ^кг/_м³;

t_м - температура мерзлых грунтов до образования чаши протаивания, приблизительно равная t₀.

Протаивание под краем сооружения h_к определяется по формуле (III-55) с понижающими коэффициентами для северной зоны 0,55, для средних районов области распространения вечномерзлых грунтов 0,65 и для южных 0,80.

Наибольшая скорость протаивания грунтов под подошвой фундамента V_h принимается численно равной глубине протаивания за 1 год:

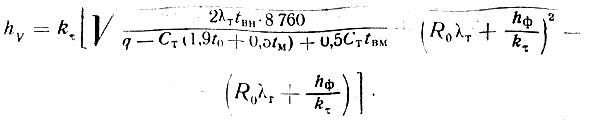
(III-56)

Удобен комбинированный способ расчета. По номограммам М. Д. Головко (рис. III-50) определяются очертание стабилизировавшейся чаши протаивания и ее максимальная глубина h_от.

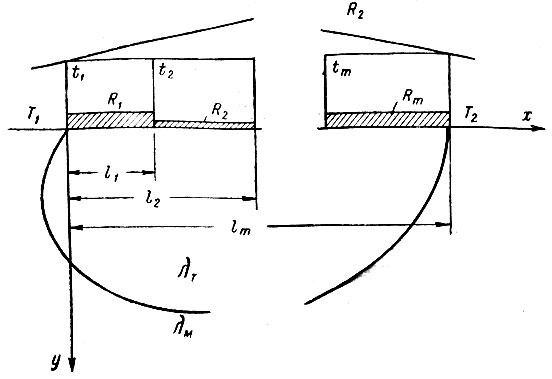
Рис. III-52. Схема краевых условий по Г. В. Норхаеву

По формуле (III-55) определяется глубина протаивания за различные сроки и строится график h = f(x) до значения h_от.

Расчетное уравнение Г. В. Порхаева:

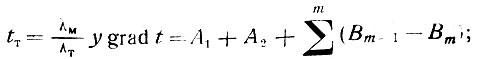
(III-57)

в этом уравнении

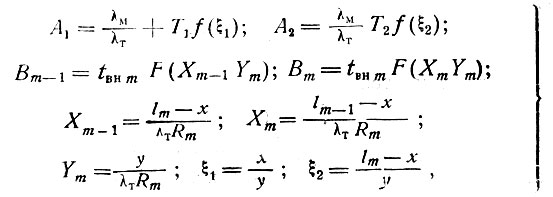
(III-58)

где t_T - температура таяния грунта;

λ_т и λ_м - коэффициенты теплопроводности грунта в талом и мерзлом состояниях в ^ккал/_{м×ч×град};

grad t - градиент температуры вечномерзлых грунтов в °С/м;

x и y - координаты кривой протаивания;

1, 2, ..., m - порядковый номер помещений, отличающихся внутренней температурой или термическим сопротивлением пола;

t_вн.1, t_вн.р, t_вн.т - внутренние температуры помещений в °С;

R₁, R₂, ..., R_m - термическое сопротивление пола в ^{м2×ч×град}/_ккал;

l₁, l₂, ..., l_m - расстояния от начала координат до точек раздела участков 1, 2,..., m в м;

Т₁ и Т₂ - температуры поверхности грунта слева и справа от сооружения.

Уравнение (III-57) решается графически; левая часть уравнения обозначается β₁, а правая β₂. Сначала подставляем известные значения величин в левую часть уравнения (III-57):

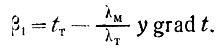
Обычно принимается

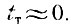
На вспомогательном графике строим прямую ОД отвечающую линейному уравнению для β₁ (рис. III-53).

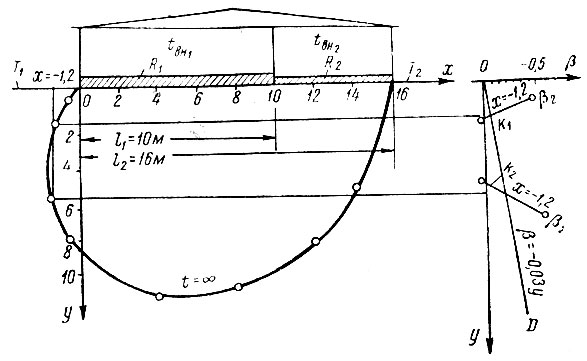
Рис. III-53. Схема решения по Г. В. Порхаеву

Определяем величины, необходимые для построения кривой β₂. Для этого задаемся координатами, например, 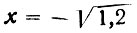и y = 1,0 м.

По номограмме находим f(ξ) для указанных выше значений x и y: на левой вертикали - точку е, соответствующую х, на правой - точку L, соответствующую y, и соединяем их прямой, которая на средней вертикали в точке М отсекает искомую функцию; на номограмме положительным значениям х соответствуют положительные значения f(ξ), отсчитываемые по шкале справа; отрицательные значения отсчитываются по левой шкале. Аналогично находим значение этой функции для точки с координатами l_m-x и y. В примере показана f(ξ) при l_m = 16; l_m-x = 17,2; y = 1 м.

По формулам (III-58) или номограмме (рис. III-54) определяем А₁ и A₂, имеющие всегда отрицательные значения. Далее вычисляем значения Х₀, Х₁ и Y₁ для левого помещения по формулам (III-58). Положим, Х₀ = 4,65; X₁ = 0,5; Y₁ = 0,42; для получения значений Х₀, Х₁ и Y₁ при заданной t_вн находим значения B₀ и B₁ по номограмме (рис. III-54).

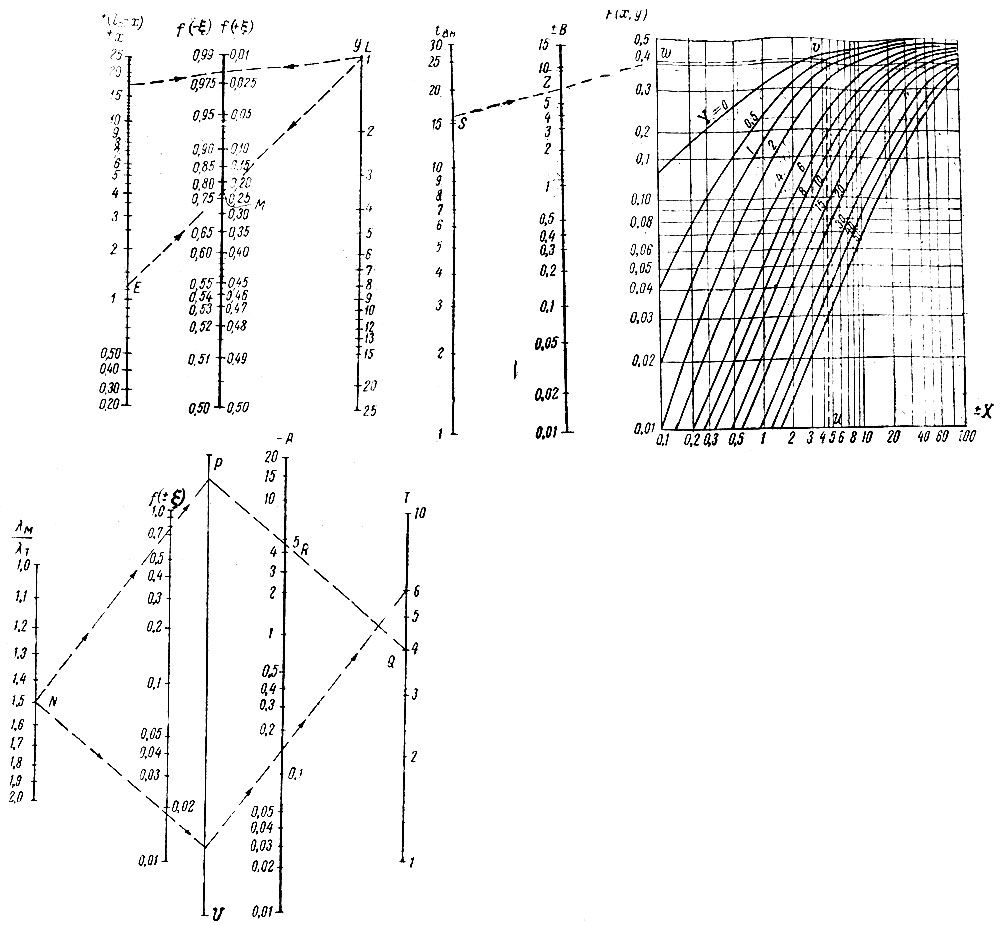
Рис. III-54. Номограммы Г. В. Порхаева

Для примера на этой номограмме показано определение В₀ при t_вн1 = 16°С. Значение t_вн1 откладываем по крайней слева вертикали (точка S). Затем на оси абсцисс находим Х₀ = 4,65. Из найденной точки U восстанавливаем перпендикуляр до пересечения с кривой Y = 0,42 в точке V и по ней находим на оси ординат точку W.

Прямая, соединяющая точки S и W, отсекает в точке z на второй слева вертикали искомое значение В₀ = 6,8; аналогично находим В₁ = 2,5.

В том же порядке вычисляем Х₁, Х₂ и Y₂ и по номограммам находим В₁ и В₂. По найденным значениям А и В определяем β₂.

Затем составляем табл. III-33 для точки с принятым значением X.

Таблица III-33. Расчет чаши протаивания

Результаты вычислений, выполненных в качестве примеров, занесены в первую строку таблицы для значения y = 1; эти данные позволяют получить значения β₂. Далее при том же значении х выполняются вычисления при произвольно возрастающих значениях y, необходимых для построения кривой β₂ и графического решения уравнения (III-57). Так, например, при y = 1, 2, 5, 7 получились следующие значения β₂ = 0,46; 008; 0,05; -0,60.

На вспомогательном графике (рис. III-53) строим отрезки кривой β₂. Кривая β₂ пересекает кривую β₁ в точках k₁ и k₂, где β₁ = β₂, и удовлетворяется уравнение (III-57); корнями уравнения являются ординаты этих точек уст.

Проектируя точки k₁ и k₂ на вертикаль с абсциссой x = -1,2 м, которым задались ранее, получаем две точки кривой чаши протаивания.

Продолжаем вычисления для других точек при значениях x, отвечающих выбранной сетке построения чаши протаивания.

Решение С. В. Томирдиаро для одного сооружения имеет вид

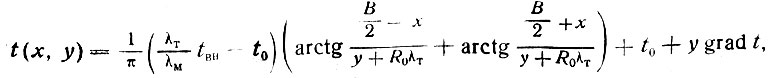
(III-59)

где t (x, y) - температура в °С для точки с координатами x, y; остальные величины те же.

Начало координат принято в точке пересечения оси поперечного сечения здания с поверхностью грунта. Пример построения температурного поля показан на рис. III-55.

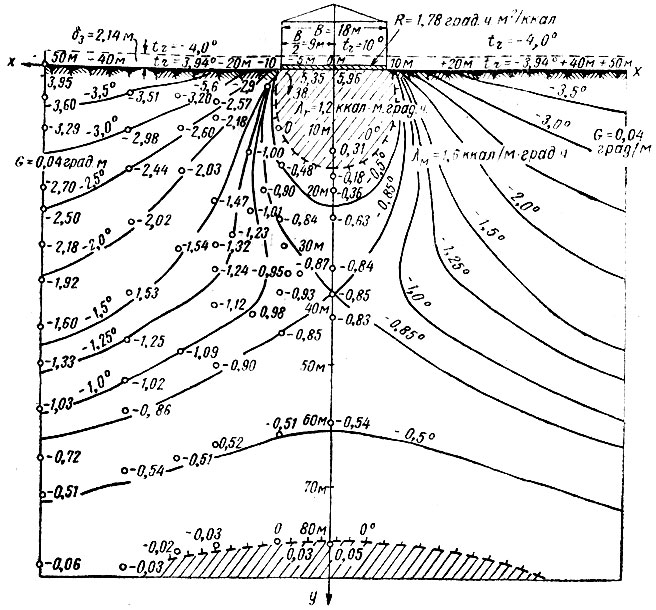
Рис. III-55. Пример построения температурного поля по С. В. Томирдиаро

В решении С. В. Томирдиаро предполагается поверхность грунта условно поднятой на величину R₀λ_т, что несколько искажает очертание боковой ветви кривой чаши протаивания у наружных стен.

Если пренебречь значением y grad t, то уравнение может быть решено относительно у в характерных точках из условия t (x, y) = 0.

Для середины здания

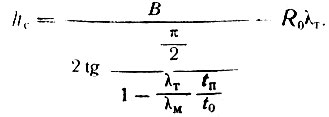
(III-60)

Для его края

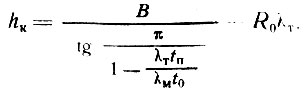
(III-61)

Чалки http://komplektacya.ru/gruzopodjemnoe-oborudovanie/stropy-gruzovye/universalnye-kanatnye/