§ 4. Усилия в каменных самонесущих стенах

Изложенная методика расчета применима для определения усилий в каменных самонесущих стенах гражданских зданий. Рассмотрим в начале усилия, возникающие в поперечных стенах и обусловленные криволинейным очертанием границы протаивания.

Для определения зоны пластических деформаций основания В_п воспользуемся уравнением:

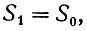
(II-38)

где S₀ и S₁ - осадки стены в краевых точках участка ^B_y/₂.

Второе уравнение получаем из условия равновесия

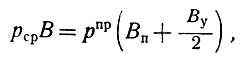
(II-39)

обозначим

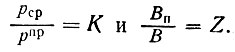
Предположим, что при определении осадок в точках 0 и 1 среднее бытовое давление принимается одинаковым (рис. II-82); подставляя значения осадок в (II-38), получим

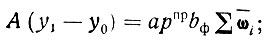
(II-40)

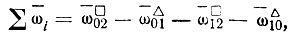
(II-41)

где ωā_i - коэффициенты, определяемые по графикам или таблицам механики грунтов (рис. II-83);

y₁ и y₀ - глубины протаивания под фундаментом в точках 1 и 0;

А, а - деформативные характеристики оттаивающего грунта;

b_ф - ширина ленточного фундамента.

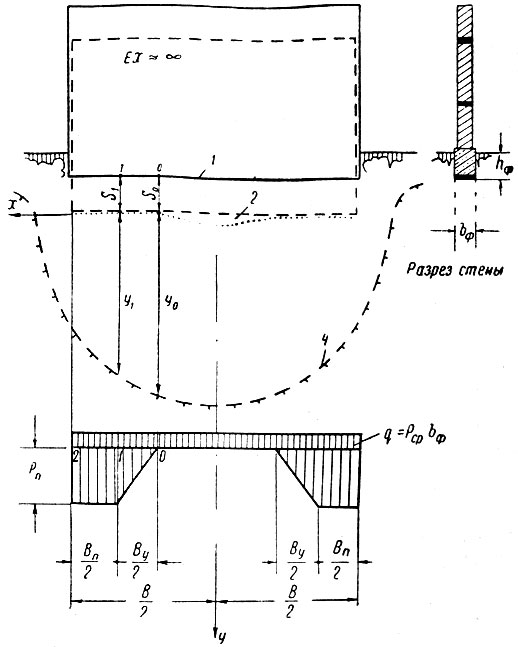
Рис. II-82. Расчетная схема поперечной стены на протаивающем основании. 1 - подошва до осадки; 2 - то же, после осадки; 3 - поверхность основания после осадки; 4 - граница протаивания

Принимая 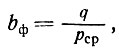где q - нагрузка на 1 пог. см стены, преобразуем уравнение (II-40) и получим

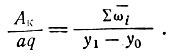
(II-42)

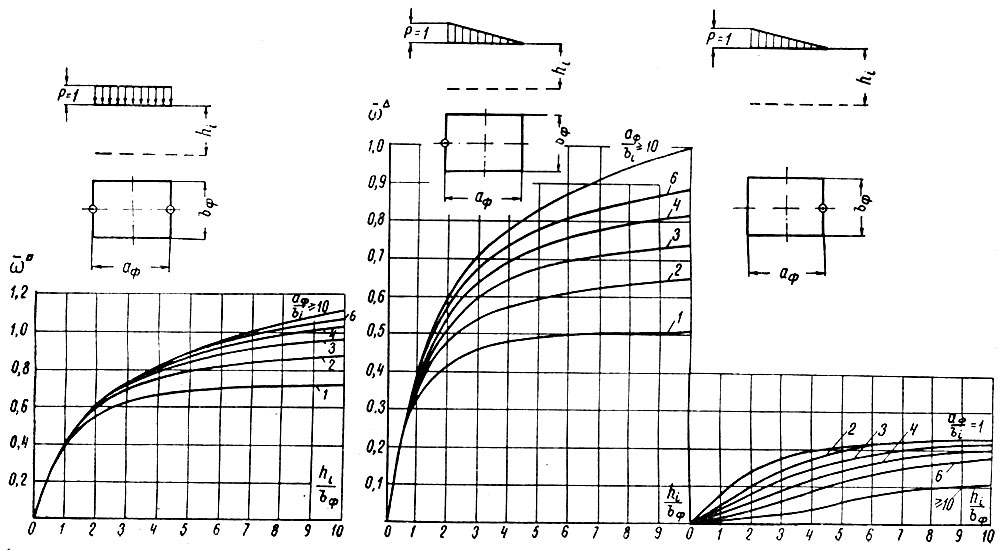
Рис. II-83. Графики для определения коэффициентов

В это уравнение входит не само неизвестное Z, а его функции. Поэтому необходимо задаться несколькими произвольными значениями Z и вычислить величины ∑ω_i, и y₁-y₀, воспользовавшись ими для графического решения уравнения; по частным значениям этих величин, при которых удовлетворяется уравнение (II-41), находим Z, а затем В_п. Значение В_y определяется из уравнения (II-38); таким образом, становятся известными все составляющие эпюры реакций основания. Значения ωā_i, необходимые для вычисления ∑ω_i, находятся из графика (рис. II-83), а величины (y₁-y₀) определяются по графикам М. Д. Головко или из уравнения С. В. Томирдиаро:

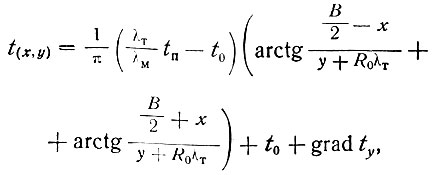
где λ_т и λ_м - коэффициенты теплопроводности грунта в талом и мерзлом состояниях;

t, t_n - температура грунта на уровне нулевых годовых амплитуд и температура воздуха на уровне пола;

R₀ - термическое сопротивление пола;

grad t_y - геотермический градиент.

Пренебрегая grad t_y при t_{x, y} = 0, получаем уравнение нулевой изотермы

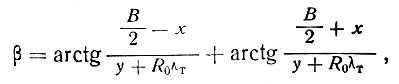
где

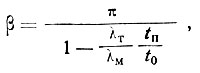
или

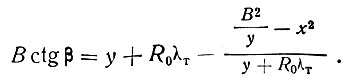
(II-43)

Решая эти уравнения относительно у, получим ординаты чаши протаивания, измеренные от поверхности:

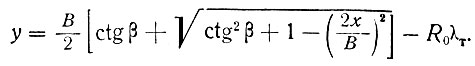
Переходя к глубине протаивания под фундаментами и подставляя значения

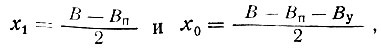
определяем значения y₁ и y₀:

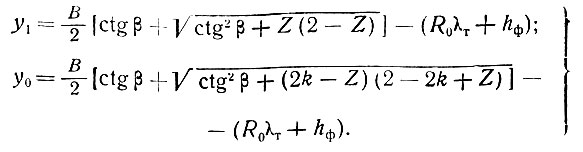
(II-44)

В качестве второго примера определим дополнительные усилия, вызванные неравномерной сжимаемостью грунтов при оттаивании. Предположим, что глубина протаивания не изменяется по длине стены; это может иметь место для продольных стен средних отсеков здания (между осадочными швами). Стена может деформироваться по схеме прогиба или выгиба, поэтому оба случая должны быть рассмотрены раздельно (рис. II-84).

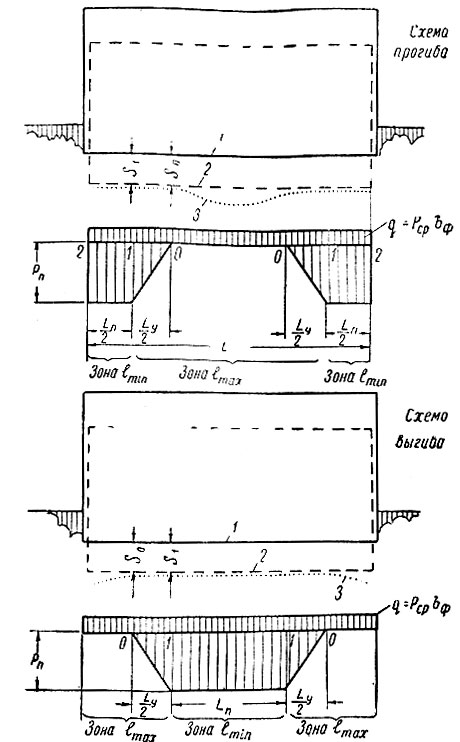
Рис II-84. Расчетная схема продольной стены среднего отсека здания на протаивающем основании. 1 - подошва до осадки; 2 - то же, после осадки; 3 - поверхность основания

Уравнение деформаций при тех же упрощенных условиях, что и в первой задаче, имеет вид:

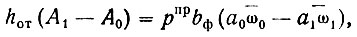
(II-45)

где A₁ и A₀, а₀ и а₁ - крайние значения деформативных характеристик;

h_от - глубина протаивания под фундаментом.

Для схемы прогиба

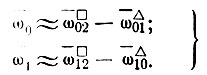
(II-46)

Для схемы выгиба

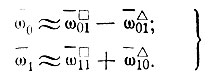
(II-47)

Подставим в (II-45) значения

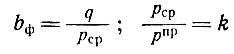
и получим

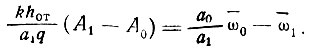
Для решения этого уравнения необходимо задаться различными значениями Z_п, вычислить соответствующие им значения Z_y = 2 (kZ - Z_п), определить ωā₀ и ωā₁ и решить уравнение аналитически или графически.