§ 3. Усилия в каркасных зданиях

Различная глубина протаивания под краями фундаментов обусловливает неравномерные осадки. Поворот опорного сечения колонны вызывает дополнительные усилия; чем больше ее жесткость, тем значительнее эти усилия. С другой стороны увеличение жесткости снижает угол поворота фундамента. При определении указанных усилий можно допустить, что на ширине подошвы фундамента компрессионные характеристики грунта не изменяются. В качестве примера определим усилия в колоннах одноэтажного промышленного здания (рис. II-81).

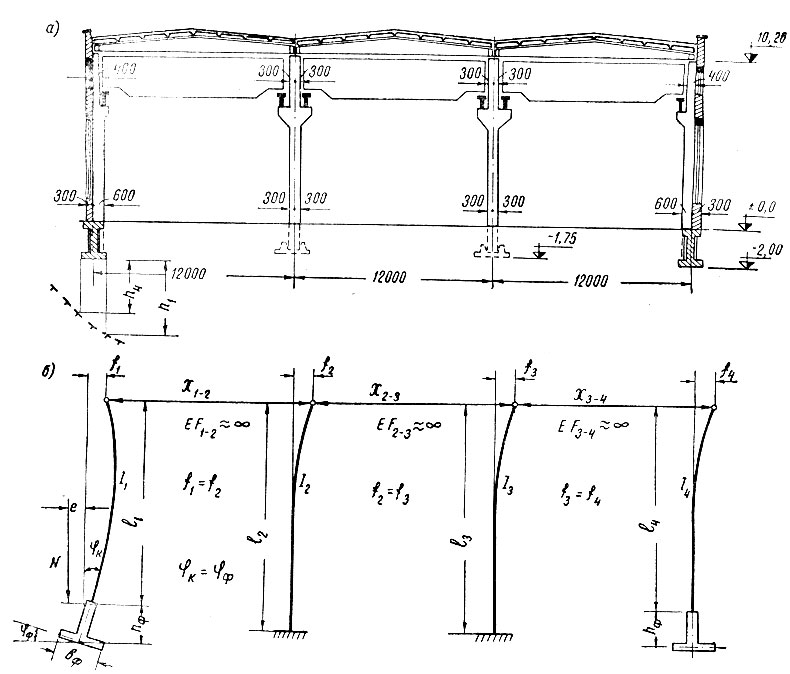
Рис. II-81. Промышленное здание на протаивающем основании. а - конструктивная схема; б - расчетная схема

Исходные уравнения для решения системы:

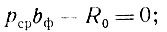
(II-24)

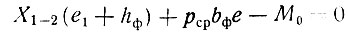
(II-25)

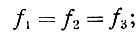
(II-26)

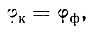
(II-27)

где p_ср - среднее давление на подошву фундамента от вертикальных нагрузок;

b_ф - ширина фундамента;

R₀ и М₀ - равнодействующая реакции основания и ее момент относительно оси фундамента на 1 пог. см длины фундаментной ленты;

X_1-2 и X_2-3 - усилия в ригелях, приходящиеся на 1 пог. см длины здания.

Смещения, входящие в уравнения (II-26):

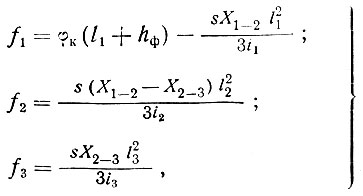
(II-28)

где s - шаг колонн вдоль фундаментной ленты.

Из условия (II-28) получаем

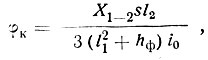
(II-29)

где i₀ - погонная жесткость системы, приведенная к погонной жесткости крайней колонны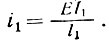

Погонная жесткость

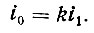
)(II-30)

При трех колоннах

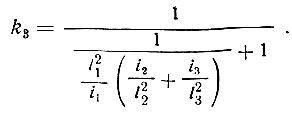
(II-31)

При двух колоннах

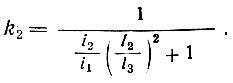
(II-32)

Для одной колонны с шарнирным закреплением верха k₁ = 1. При других конструктивных схемах зависимость φ_к от Х_1-2 может быть получена аналогичным способом и приведена к виду (II-29).

При малом значении угла

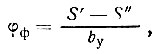
(II-33)

где S' и S" - осадки фундамента под краями зоны уплотнения шириной b_y, которые определяются из уравнения:

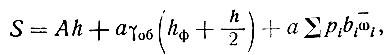
(II-34)

где h - глубина протаивания под подошвой фундамента в см;

γ_об - объемный вес грунта в ^кг/_см³;

b_i - ширина части -подошвы фундамента, на которую передается давление интенсивностью p_i, в ^кг/_см²;

ωā_i - коэффициенты, зависящие от отношении ^а_ф/_bi и ^h/_bi, определяемые по графикам (рис. III-57). Эти коэффициенты обозначаются: с верхними индексами в виде прямоугольников или треугольников в зависимости от формы эпюры реактивных давлений и с нижними - двумя цифрами, первая из которых означает точку, для которой определяется ωā_i, а вторая - другую точку, где кончается эпюра реактивных давлений (см. табл. II-32).

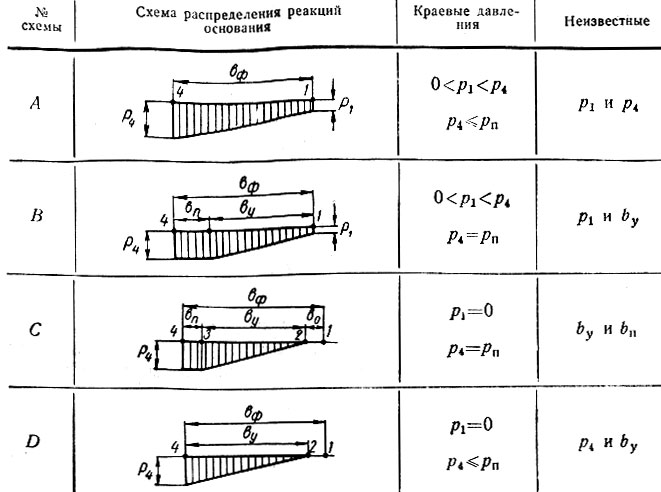
Таблица II-32 Эпюры реактивных давлений

Подставляя значения осадок (II-34); получим угол поворота фундамента

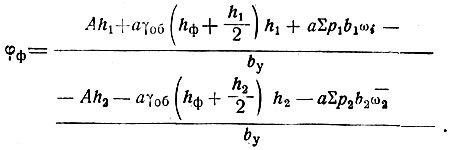
(II-35)

Здесь индексами 1 и 2 обозначены величины, относящиеся к краям зоны b_y.

Зная значения φ_ф по (II-35) и φ_к по (II-29), решим систему уравнений (II-24), (II-25) и (II-27); результаты этих решений для всех четырех схем реактивных давлений приведены в табл. II-33.

Таблица II-33. Формулы для определения краевых давлений и дополнительных усилий в ригелях

Для схемы А уравнение решено относительно краевых давлений p₁ и р₄. Другие схемы включают b_i как неизвестные, поэтому для каждой из них уравнение решается графически или подбором.

Значения ωā_i входящие в эти формулы, определяются по графикам (рис. III-57) при значениях ^а_ф/_bi и ^h/_bi, указанных в табл. II-34.

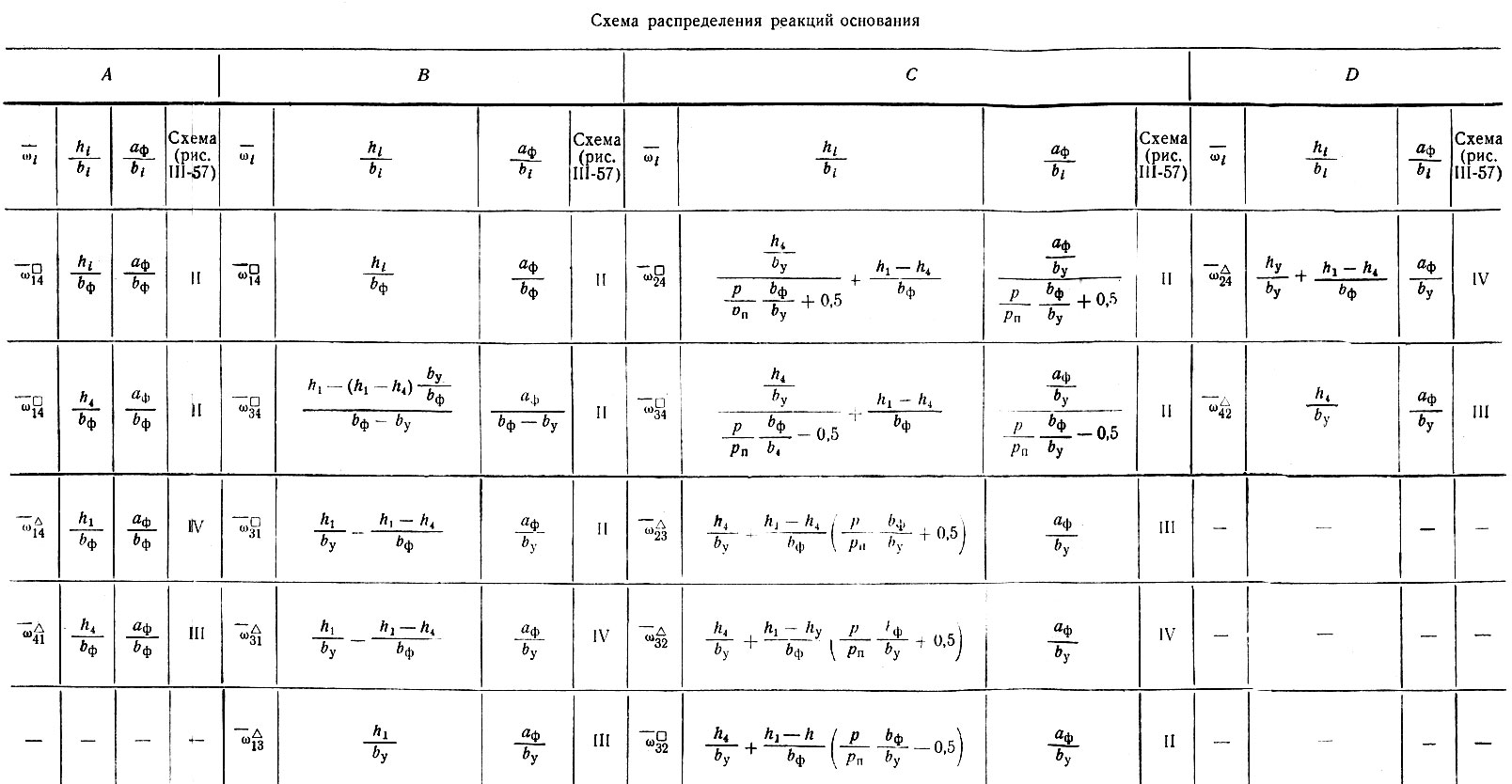
Таблица II-34. Данные для определения ωā_i

После того, как определено усилие в ригеле Х_1-2 s, вычисляются крен фундамента φ_ф и усилие в другом ригеле по формулам, общим для всех схем распределения давлений:

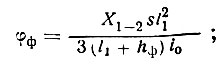
(II-36)

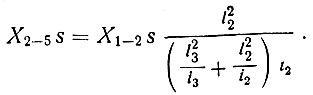
(II-37)

Этим же решением можно воспользоваться для определения усилий, когда колонны опираются на отдельные фундаменты с подошвами а_ф×b_ф. В этом случае значения ωā_i устанавливаются по тем же графикам при данных, указанных в табл. II-34, а усилия в ригелях получаются умножением Х_1-2 и Х_2-3 не на s, а на а_ф. При этом следует заметить, что в формулах, определяющих коэффициенты D, значения s сохраняются.

Расчет производится в следующем порядке:

1. Вычисляется предельное давление р^пр по формулам (II-22) и (II-23).
2. Определяются краевые давления по схеме А (табл. II-32). Для этого вычисляют коэффициенты D₁ и D₂ (табл. II-33) и определяют ω₁₄ и ω₄₁ по графикам (рис. III-57) при данных, указанных в табл. II-34. По формулам табл. II-33 вычисляют значения р₄ и р₁.
3. Полученное значение максимального краевого давления р₄ сопоставляют с р^пр. Если р₄≤p^пр, а p₁≥0, то расчет продолжается по схеме А; если это условие не соблюдается, выполненный расчет оказывается лишь предварительным и его необходимо продолжить по другой схеме распределения реакций.

Пример. Требуется определить усилия в конструкциях одноэтажного двухпролетного промышленного здания, вызываемые неравномерным протаиванием под фундаментами крайней колонны. Колонны железобетонные из бетона М-200. Сечение крайних колонн 40×60, средних - 80×40 см; шаг S = 6 м; высоты l₁ = 9 и l_e = 14 м.

Среднее давление на подошву p_ср = 4 ^кг/_см², эксцентриситет равнодействующий е = 0,15 м. Глубина заложения подошвы h_ф = 3,5 м, ее ширина b_ф = 1,2 м. Основание сложено песчаным грунтом с характеристиками:

Глубины протаивания под краями подошвы h₁ = 3,5 м, h₄ = 2,3 м. Предельное давление вычислено по формулам (II-22 и II-23) и оказалось равным 12,5 ^кг/_см².

Вычисляем погонные жесткости:

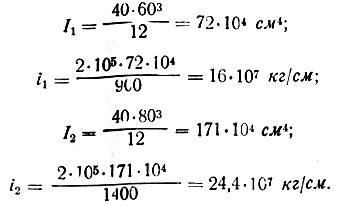
Коэффициент жесткости по (II-31)

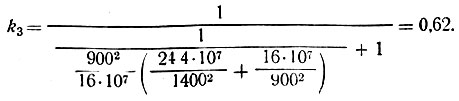
Приведенная погонная жесткость (II-32)

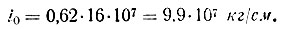
Как указано выше, расчет следует начинать по схеме A (табл. II-30). Коэффициенты по табл. II-33:

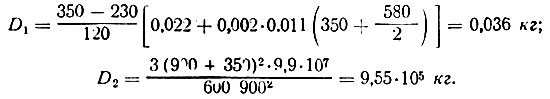
По табл. II-34 устанавливаем значения, определяющие ωā:

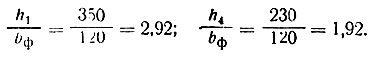
По графику (рис. III-57) для ленточных фундаментов

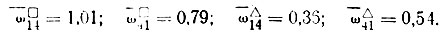
Краевые давления по формулам табл. II-33

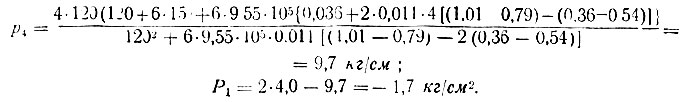
Так как p₁<0, то условия схемы A не соблюдаются, поэтому продолжаем расчет по схеме D. Вычисляем коэффициенты для этого случая по формулам табл. II-33; D₇ = -0,138, D₈ = 0,002 ¹/_см. Из табл. II-33 (вклейка) имеем:

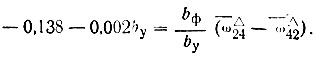
Уравнение решаем графически, задавшись несколькими значениями 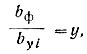например, y' = 1; y" = 2; необходимо предварительно определить функции игреков - коэффициенты ωā, пользуясь графиком рис. III-57 и табл. II-34 (вклейка). Значения этих коэффициентов приведены в табл. II-35.

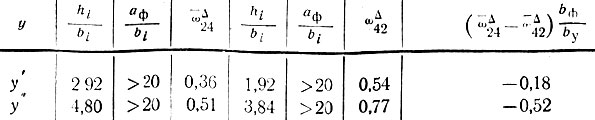
Таблица II-35. Определение коэффициентов ωā

Обозначим левую часть уравнения - 0,138-0,002 b_y = U_л и правую 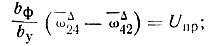определим их значения при принятых y' = 1 и y" = 2 (табл. II-36).

Таблица II-36. Значения U_л и U_пр

Абсцисса точки пересечения кривых U_л = f(у) и U_пр = f(y) дает искомое значение y = ^b_ф/_by = 1, 34; для краткости произведен расчет по двум значениям y, однако для получения более точного решения следовало бы взять еще по крайней мере одно промежуточное значение.

По формулам табл. II-33 краевое давление

p₂ = 2×4×1,34 = 11,4 ^кг/_см²<p^пр = 12,5 ^кг/_см², т. е. условия схемы D соблюдаются; при b_y = ¹²⁰/_1,34 = 90 см усилие в ригеле 1-2

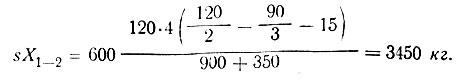
Крен по (II-36)

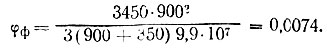
Усилие в другом ригеле по (II-37)

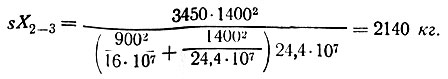
Горизонтальная нагрузка на среднюю колонну

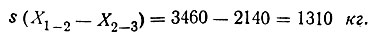
Расчет показывает, что при неравномерном протаивании основания возникают значительные дополнительные усилия, для уменьшения которых следовало бы, по возможности, увеличить значение ^p_ср/_p^пр.