Б. Элементы составного сечения

Из элементов составного сечения для пластмасс наибольшее практическое значение имеют стеновые панели и плиты покрытий, составляемые обычно из различных материалов.

Растянутые элементы, составленные из разных материалов, рассчитываются принципиально так же, как и сплошные, т. е. по формуле (7), но при подсчете площади поперечного сечения нетто все составные части его приводятся к одному материалу. Так, если элемент составлен из двух материалов, занимающих каждый части сечения F₁ и F₂, то приведенное значение общей площади поперечного сечения F_пр равно

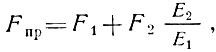(20)

где Е₁ и Е₂ - модули деформаций соответствующих материалов.

Сжатые элементы составного из разных материалов сечения на прочность рассчитываются так же, как и растянутые, но по формуле (9).

Наиболее неблагоприятные результаты дает, однако, расчет сжатых элементов на устойчивость. Применительно к конструкции трехслойных панелей и плит с обшивками из высокопрочных материалов и рабочим средним слоем (заполнителем) из пенопласта или другого легкого материала, имеющего модуль сдвига до 500 кГ/см² (рис. 17), расчет на устойчивость при действии равномерно распределенной нагрузки производится по следующим формулам [8].

Критическая нагрузка Т_кр, отнесенная к единице ширины одной обшивки, вычисляется из выражения

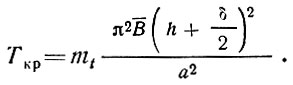(21)

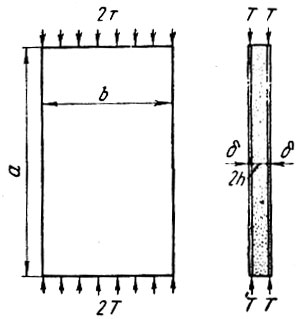
Рис. 17. Расчетная схема трехслойной панели при центральном сжатии

Коэффициент m_t оценивает способ закрепления обшивки по периметру и зависит также от отношения размера а - обшивки в направлении действующего усилия к поперечному размеру b. Для трехслойных плит и панелей принимается [9] наиболее неблагоприятная схема бесконечно широкой пластинки, дающая минимальное значение коэффициента m_t равное

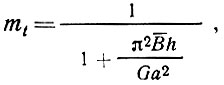(22)

где G - модуль сдвига материала среднего слоя;

h - половина его толщины;

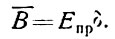(23)

Величина В̄ характеризует в кГ/см жесткость обшивки. Формула (21) применима при соблюдении условий:

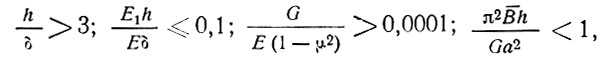
где Е₁ - модуль деформаций заполнителя. При других условиях коэффициент m_t имеет другое значение [8].

Разделив критическую силу на толщину обшивки, получим критическое напряжение. Подставив в (21) значение В по формуле (23), получим

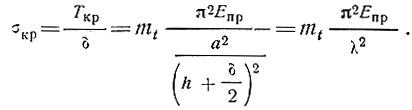(28)

Знаменатель полученного выражения является квадратом гибкости трехслойной плиты, так как а = l₀ - расчетной длине и

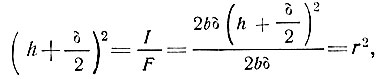
где r - радиус инерции, подсчитанный приближенно и без учета среднего слоя, принимающего слабое участие в восприятии сжимающей силы ввиду своей легкости. Но средний слой воспринимает сдвигающие напряжения, когда произойдет выпучивание элемента при потере устойчивости, что учитывается коэффициентом m_t.

Величина

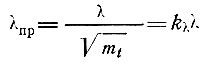(25)

называется приведенной гибкостью составного трехслойного элемента с легким заполнителем, причем коэффициент гибкости k_λ с учетом выражений (22), (23) и (24) равен

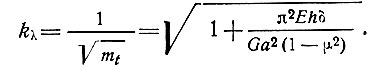(26)

Подсчитанный аналогичным образом коэффициент гибкости трехслойного элемента цилиндрической формы (например, в своде) равен [9]

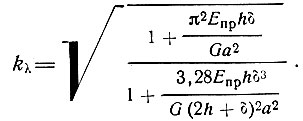(27)

Он несколько меньше, чем у плоского элемента.

Вычисленная критическая сила (или критическое напряжение) сравнивается с действующей силой, которая относится только к обшивкам в пренебрежении заполнителем. Обозначим

а общее усилие, действующее на панель вдоль ее вертикального размера, через N, тогда

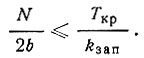
Коэффициент запаса k_зап принимается равным 1,5-2, в зависимости от капитальности сооружения.

Помимо потери общей устойчивости, возможно местное выпучивание обшивки, сопровождающееся отрывом от среднего слоя или вдавливанием в него. Критическое напряжение отрыва (в направлении, перпендикулярном обшивке) определяется при этом по формуле

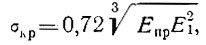(28)

где Е₁-модуль деформаций материала среднего слоя.

Критические напряжения, вычисляемые по этой формуле, достаточно велики и в обычных случаях проверка их не делается. Необходимость в использовании формулы (28) возникает при учете начальной погиби обшивки (см. пример 13).

Изгибаемые элементы составного сечения (плиты, панели) различаются по конструкции на ребристые и сплошные.

Ребристые плиты и панели рассчитываются по формулам сопротивления материалов, исходя из приведенной ширины полосы - b_пр, равной [10]

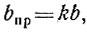
где b - действительное расстояние между продольными ребрами, расположенными вдоль пролета; k - коэффициент неравномерности распределения нормальных напряжений по ширине полосы, берется по графику (рис. 18) в зависимости от отношения пролета к расстоянию между ребрами.

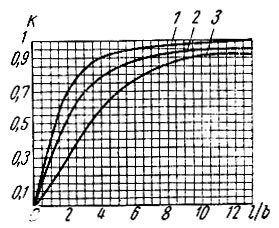
Рис. 18. Графики коэффициента неравномерности для расчета ребристых панелей (плит): 1 - для изотропных материалов (асбестоцемента, алюминиевых сплавов, полиэфирного стеклопластика); 2 - для КАСТ-В; 3 - для фанеры

Расчет на прочность по нормальным напряжениям производится по формуле

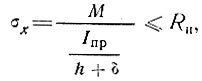(30)

где М - расчетное значение изгибающего момента от нагрузки, действующей в полосе шириной h - половина высоты среднего слоя;

δ - толщина обшивки;

I_пр - момент инерции, вычисленный по приведенной ширине полосы, включающей одно ребро.

Если ребра выполнены из другого материала, то их сечение приводится к материалу обшивок за счет толщины при сохранении прежней высоты сечения.

Расчет на прочность по напряжениям скалывания производится по формуле

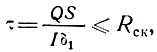
где ₁ - толщина ребра, или ширина клеевого шва между ребром и обшивкой;

R_ск - расчетное сопротивление на скалывание материала ребра, или на сдвиг клеевого шва;

S - статический момент сдвигаемой части сечения.

При подсчете момента инерции и статического момента делается приведение элементов сечения к одному материалу.

Проверка по прогибам производится по формулам сопротивления материалов по нормативным нагрузкам и приведенному моменту инерции, вычисляемому исходя из приведенной ширины полосы, выделенной для расчета.

Устойчивость сжатой обшивки проверяется путем вычисления критической силы T_кр и сравнения ее с фактической по формулам (12) и (13).

Кроме расчета плиты (панели) на прочность и прогиб, производится расчет наружной обшивки на местный изгиб в пролете между продольными ребрами или поперечными. За расчетную схему принимается неразрезная балка. Проверяются нормальные напряжения и местный прогиб. Нормальные напряжения от местного изгиба могут накладываться на нормальные напряжения от общего изгиба. Допускаемые прогибы при местном изгибе принимаются не более 1 : 75 расчетного пролета.

Если к нижней поверхности обшивки подклеен слой пенопласта толщиной d, то его прочность при местном изгибе проверяется по формуле

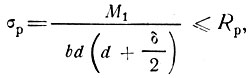
где М - максимальное значение местного изгибающего момента;

R_p - расчетное сопротивление пенопласта на растяжение.

Сжимающее напряжение в обшивке, возникающее от местного изгиба при наличии поддерживающего слоя пенопласта, сравнивается с расчетным сопротивлением материала обшивки на сжатие по формуле

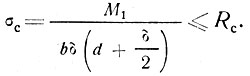(33)

Во избежание потери устойчивости обшивки, усиленной поддерживающим слоем, надо, чтобы d ≥ 30 δ.

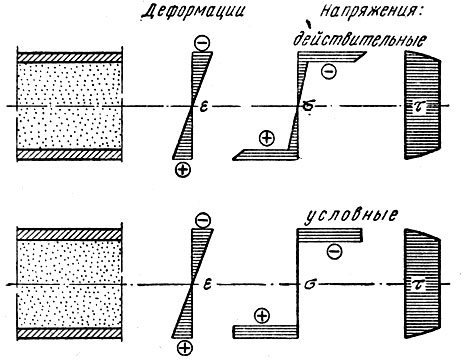
Рис. 19. Фактическое и расчетное распределение деформаций и напряжений по высоте сечения трехслойного изгибаемого элемента

Сплошные трехслойные плиты и панели составного сечения рассчитываются исходя из предположения, что все нормальные напряжения воспринимаются обшивками, а средний слой из легкого заполнителя участвует в работе только на сдвиг (рис. 19). Причем при подсчете геометрических характеристик поперечного сечения ширину пенопласта, приведенную к материалу обшивок и незначительную по величине, ввиду большой разницы между модулями деформаций материалов заполнителя и обшивок, принимают равной нулю.

В случае равномерно распределенной нагрузки и свободного (шарнирного) опирания плиты формулы для расчета на прочность имеют вид:

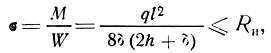(34)

по нормальным напряжениям

по напряжениям сдвига

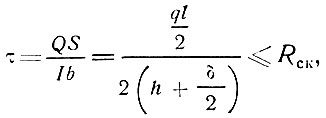(35)

где R_и - расчетное сопротивление на изгиб обшивок; ,

R_CK - расчетное сопротивление на сдвиг заполнителя или клеевого шва между заполнителем и обшивками. Прогибы проверяются по формуле А. И. Брусиловского [10] с учетом сопротивления сдвигу среднего слоя

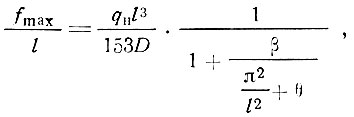(36)

где цилиндрическая жесткость равна

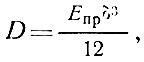
а величины β и θ находятся по формулам

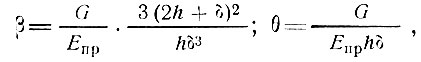
где G - модуль сдвига заполнителя.

Вычисления показывают, что единицей в знаменателе выражения (36) можно пренебречь. Тогда оно принимает вид [9]

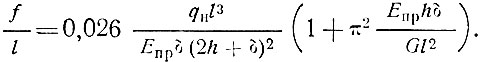(37)

По структуре уравнение (37) совпадает с формулой (17) для прогиба балки сплошного сечения.

При пользовании формулами (34-37) все размеры берутся в сантиметрах, а нормативная нагрузка относится к погонному сантиметру полосы шириной 1 см, выделяемой для расчета, т. е. в конечном счете к 1 см² поверхности плиты.

Сжато-изгибаемые элементы составного сечения рассчитываются на прочность по нормальным напряжениям по формуле (18). При расчете ребристых плит и панелей коэффициент ф принимается для материала обшивок (см. ч. III), причем материал ребер приводится к материалу обшивок.

При расчете трехслойных плит и панелей с легким заполнителем на прочность по нормальным напряжениям также используется формула (18), но коэффициент ξ определяется по отношению действующей силы N к критической

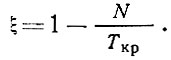(38)

Критическое значение нагрузки T_кр вычисляется исходя из формул (24-27)

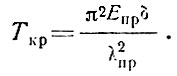(39)

При этом все геометрические характеристики F_нт, W_нт, λ вычисляются без учета заполнителя для полосы шириной b = 1 см.

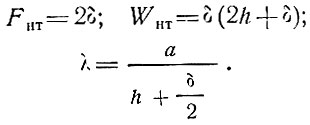
При проверке прочности по касательным напряжениям они вычисляются без учета нормальной силы.

Прогибы определяются исходя из формул (19) и (37).