Пример 14. Купол из светопроницаемых плит

Задание. Разработать сборную конструкцию светопроницаемого покрытия отапливаемого здания, имеющего в плане круглую форму. Пролет 30 м. Район строительства - Донбасс, г. Северо-Донецк.

Выбор материалов и конструкции. Рациональной формой покрытия круглого в плане здания является купольное. Принимаем для купола трехслойные плиты общей толщиной 8,4 см с обшивками из плоских листов полиэфирного стеклопластика толщиной 2 мм и средним слоем из отрезков стеклопластиковых труб высотой 8,0 см. Внутренний диаметр труб 22,0 см (рис. 77).

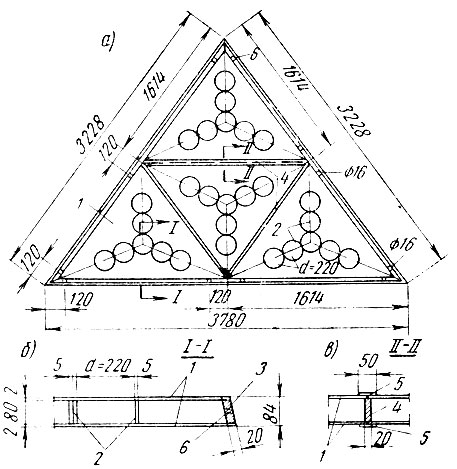
Рис. 77. Светопроницаемая плита купола: а — вид снизу, нижняя обшивка не показана; б — часть поперечного сечения; в — стык обшивок; 1 обшивка из плоского стеклопластика; 2 — кольцо из стеклопластика; 3 - несущее ребро из однонаправленного стеклопластика; 4 — деревянная прокладка; 5 — накладка из стеклопластика; 6 — отверстие для болта

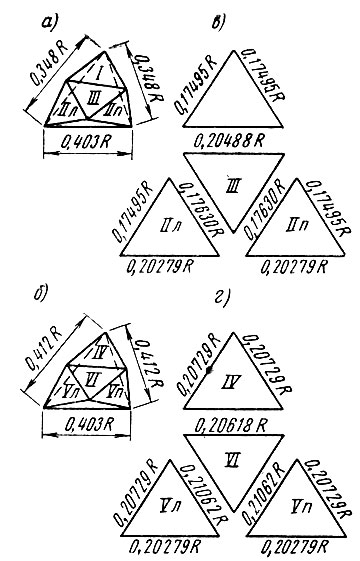
Рис. 78. Размеры сторон треугольных граней купола, вписанного в сферу 180 и 720-гранника:а — разбивка грани пятигранных пирамид 180-гранника; б — разбивка грани шестигранных пирамид 180-гранника; в-г — размеры сторон граней 720-гранника в зависимости от радиуса описанной сферы

Плиты имеют несущие ребра из стеклопластика типа АГ-4С. Размеры сечения ребра 2X8 см.

Ребра и средний слой (торцы отрезков труб) склеиваются с обшивками полиэфирным клеем.

Купольное покрытие опирается на стальное опорное кольцо соответствующей формы, сваренное из отрезков швеллера. Опорное кольцо уложено на несущие элементы каркаса здания.

Геометрические характеристики купола. Принимаем форму купола сферической. Разбивка шаровой поверхности на составные элементы различной формы производится несколькими способами [14, 15]. В рассматриваемом случае форма панели принимается плоской треугольной.

Сферическая форма поверхности при разбивке на плоские треугольные грани последовательно заменялась 20-гранником, 32-гранником, 180-гранником и наконец 720-гранником. На рис. 78, а, б пунктиром показаны треугольные грани двух типоразмеров пятиугольных и шестиугольных пирамид, образующих поверхность 180-гранника и "надстроенные" над ними треугольные грани 720-гранника шести типоразмеров. На рис. 78, в, г приведены размеры граней 720-гранника в зависимости от радиуса описанной сферы. В следующей таблице даны углы между плоскостями смежных граней.

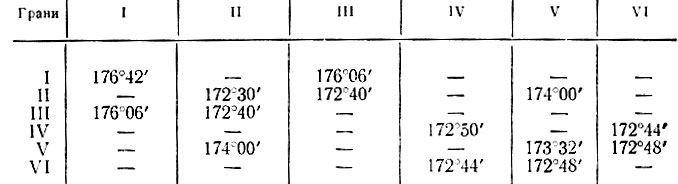
Радиус сферы R принят равным 1844,7 см. Задавшись стрелой подъема купола f = 744 см, уточняем пролет купола l и центральный угол 2α. Для купола кругового очертания следует

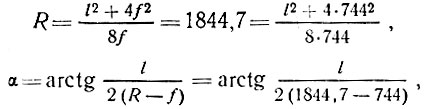
отсюда находим

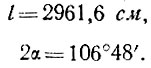
Форма купольного покрытия представляет вписанный в часть сферы многогранник, состоящий из 125 треугольных граней - плит шести типоразмеров. Основные размеры плит определяются исходя из данных, приведенных на рис. 78 и в таблице.

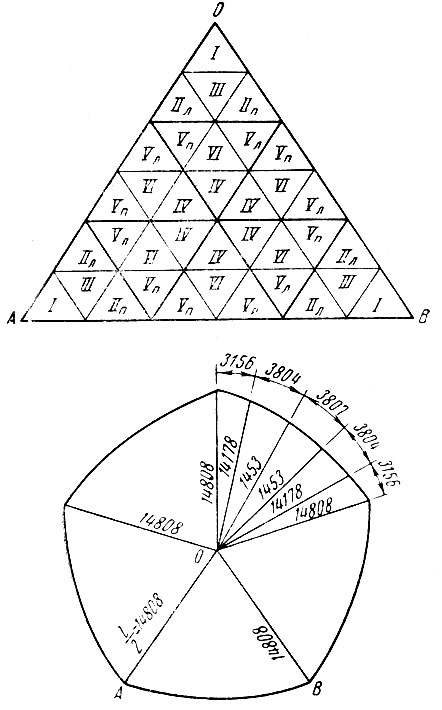
Рис. 79. Схема раскладки плит купола в покрытии и основные размеры плана на уровне примыкания панелей к опорному кольцу

Схема раскладки плит покрытия показана на рис. 79, такая раскладка повторяется пять раз.

Нагрузки. Нагрузка от собственного веса купола равномерно распределена по поверхности сферы. Средний вес одной плиты складывается "из веса обшивок - 28 кГ, колец при толщине стенки 5 мм - 29 кГ, несущих ребер из стеклопластика - 30 кГ, прочих материалов - 14 кГ. Вес 1 м² поверхности купола при площади одной плиты 5 м² равен

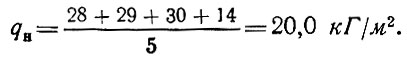
Снеговая нагрузка имеет интенсивность Я'=50 кГ/м, исчисляемую на плоскую горизонтальную поверхность. С учетом сферической формы покрытия по аналогии со сводчатой получаем

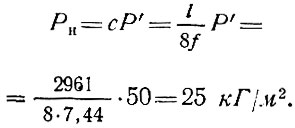
Закон распределения снеговой нагрузки на купол выражается формулой

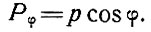
Здесь φ угол, исчисляемый в поперечном разрезе купола от вертикального положения радиуса сферы (рис. 80. а).

Ветровая нагрузка, эпюра которой представлена на рис. 80, б с некоторым приближением может быть заменена при практических расчетах суммой двух эпюр: симметричной W₁ (рис. 80, в) и кососимметричной W₂ (рис.80, г, д) нагрузки. Интенсивность ветровой нагрузки W'₀ находят при этом по формуле

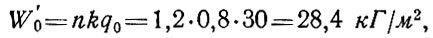
где q₀ - скоростной напор ветра по по СНиП;

n — коэффициент перегрузки;

k — аэродинамический коэффициент для вертикальной поверхности.

Продолжительность действия снеговой нагрузки принимаем 90 суток, ветровой — 3 суток. Нагрузки приводим к кратковременным, используя прочностные k_дс временные коэффициенты, которые определяем по рис. 95 для несущего материала ребер — стеклопластика типа АГ-4С.

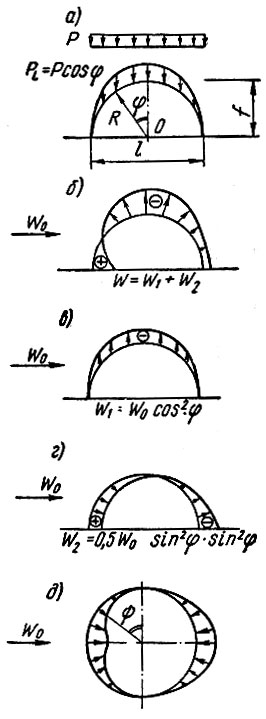
Рис. 80. Эпюры нагрузок на полусферу: а — снеговая нагрузка; б — суммарная ветровая нагрузка; в — симметричная ветровая нагрузка; г — кососимметричная ветровая нагрузка; д — распределение ветровой нагрузки в плане

Расчетная постоянно действующая приведенная нагрузка от собственного веса купола

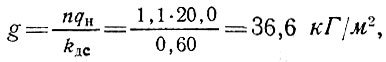
то же от снега

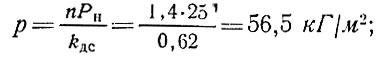
то же от ветра

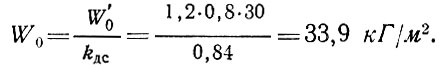
Вычисление усилий. Усилия, возникающие в конструктивных элементах купола, вычисляем в пренебрежении изгибающими моментами, т. е. по так называемой безмоментной теории. Для тонкостенных куполов сферической формы такое приближение оправдывается опытом строительства.

При воздействии на купол нагрузок в его оболочке возникают меридиональные Т₁ кольцевые Т₂ и сдвигающие S усилия. Они могут быть выражены как произведения некоторых коэффициентов на нагрузку и радиус сферы. Коэффициенты, вычисленные для различных сечений купола, представлены в виде графиков на рис. 81. Здесь построены эпюры меридиональных, кольцевых и сдвигающих усилий, а также распора Я в опорном кольце для полусферы радиусом, равным единице при единичных нагрузках. Для вычисления усилий в каком-либо сечении купола- оболочки достаточно умножить определенный по рис. 81 соответствующий коэффициент на интенсивность нагрузки и радиус сферы, а при определении распора - на квадрат радиуса сферы.

Наибольшее сжимающее меридиональное усилие действует у опорного кольца при угле φ = α = 53°,

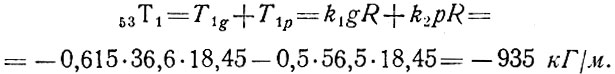
Ветровая нагрузка здесь не учитывается, так как меридиональное усилие от нее имеет противоположный знак.

У опорного кольца при угле ψ = 180° (рис. 81, 7) действует сжимающее кольцевое усилие

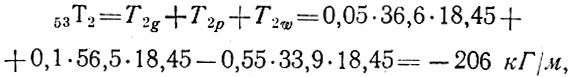
а при угле ψ = 0 растягивающее кольцевое усилие

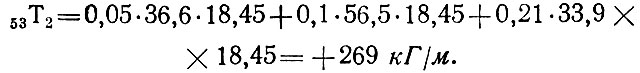
Наибольшее сжимающее кольцевое усилие находим у вершины купола

Такую же величину имеет у вершины купола и меридиональное усилие

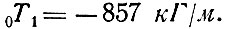
Наибольшее сдвигающее усилие от кососимметричной ветровой нагрузки действует у опорного кольца

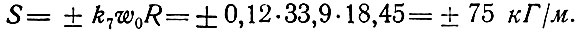
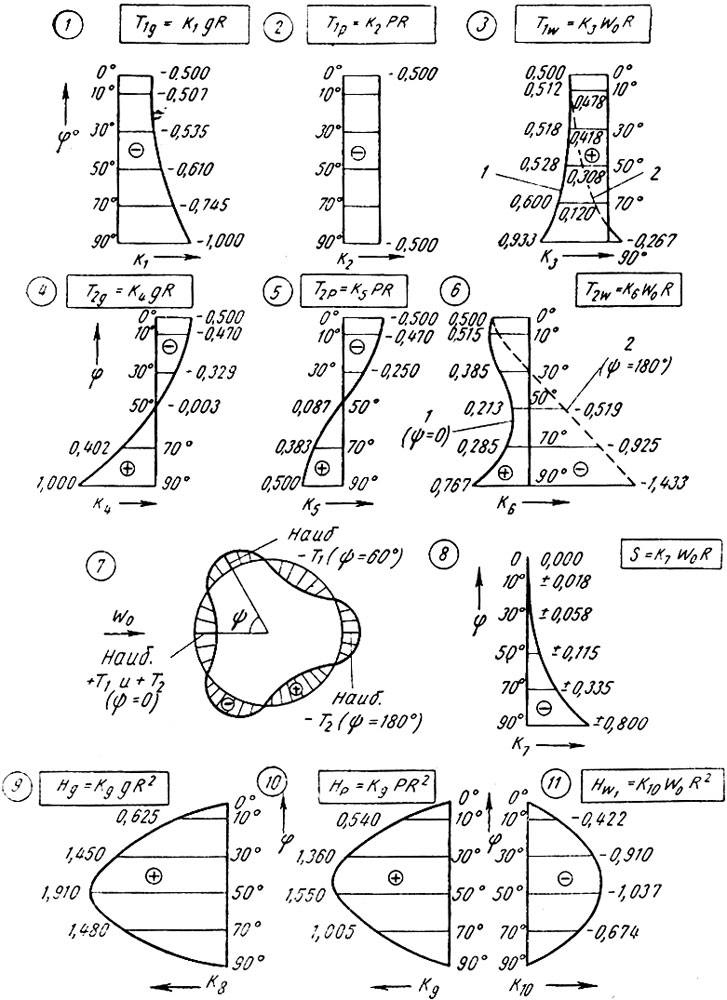
Рис. 81. Эпюры усилий в полусфере: 1 — меридиональные усилия от собственного веса конструкции; 2 — меридиональные усилия от снега; 3 — меридиональные усилия от ветра; 4 — кольцевые усилия от собственного веса; 5 — кольцевые усилия от снега; 6 — кольцевые усилия от ветра; 7 — характер распределения меридиональных и кольцевых усилий по сечениям, параллельным основанию; 8 — сдвигающие усилия от кососимметричной ветровой нагрузки; 9 — распор от собственного веса; 10 — распор от снега; 11 — распор от симметричной ветровой нагрузки

Проверка напряжений в стержнях купола. Наибольшие сжимающие усилия, как это следует из проделанного выше статического расчета, имеют место у вершины купола. Это усилие определим как равнодействующую меридионального и кольцевого усилий

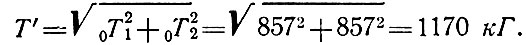
Усилие, действующее на два прилегающих друг к другу ребра смежных плит, при наибольшем размере стороны плиты 3,88 м составит

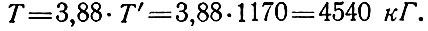
Примыкающие к этому ребру под углом другие ребра это усилие не воспринимают.

Определяем сжимающее напряжение в ребрах купола

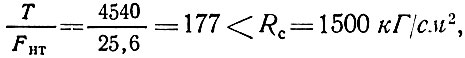
где

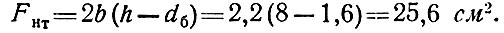
Расчет на устойчивость сферического сетчатого купола с треугольными ячейками. Явление потери общей устойчивости купола состоит в продавливании одного или нескольких узлов в направлении центра сферы (рис. 82, а). Устойчивость обеспечена, если угол ρ между основанием пирамиды, составленной из шести плит, и одной из боковых (рис. 82) граней превышает критическую величину ρ₁

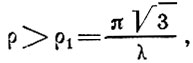
где λ - гибкость стержня;

ρ - угол наклона стержня (рис. 82, б).

В нашем случае

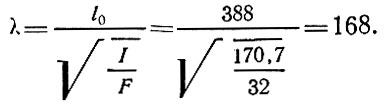
Здесь момент инерции спаренного ребра

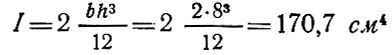
и площадь поперечного сечения спаренного ребра

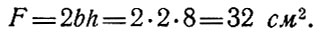
Вычисляем ρ (рис. 82, а) и сравниваем с ρ₁

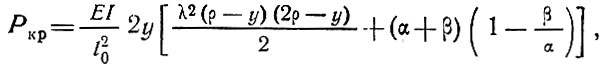
Угол ρ определяется при принятом способе разбивки сферы на 720 граней по величине его косинуса, равного отношению половины длины стороны 180-гранника к длине стороны 720-гранника.

Расчет на местную устойчивость производим с некоторым упрощением на узловую сосредоточенную нагрузку, прилагаемую к вершине шестигранной пирамиды, образованной шестью плитами купола. Схема двух звеньевой расчетной системы приведена на рис. 82, б.

Узловая критическая нагрузка для двухзвеньевой системы определяется [19] по формуле

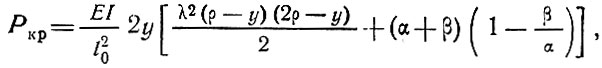
где λ = 168 - гибкость стержня;

E = 285 000 кГ/см² - модуль упругости материала ребер

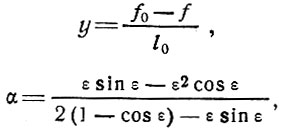
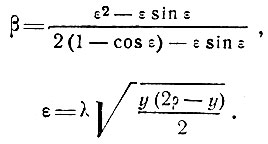
Задаваясь значением величины y, находим соответствующие значения силы Р. Построив график в координатах y-Р, найдем по максимуму величину критической силы Р_кр (рис. 82, в).

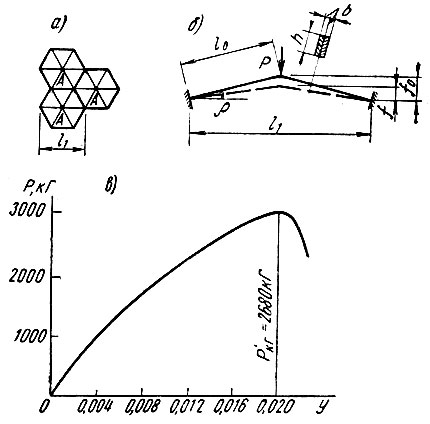
Рис. 82. Схема для определения критической нагрузки на купол: а - расположение шестигранных пирамид; б - расчетная система; в - график для определения критической нагрузки

Таким образом, критическая сила на одну двухзвеньевую систему P_к = 1690 кГ. В вершине шестигранной пирамиды сходится три двухзвеньевых системы и, следовательно, критическая сила в узле "А"

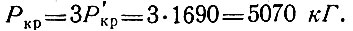
На узел "А" приходится грузовая площадь, равная двум площадям плиты. Определим нагрузку, приложенную к этому узлу

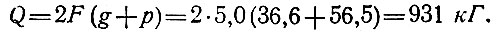
Коэффициент запаса при расчете на местную устойчивость купола таким образом составит

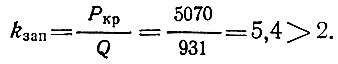
Определение прогиба и несущей способности треугольных плит при местном изгибе. Расчет плит по прогибам и на прочность при местном изгибе производим на максимальную снеговую нагрузку у вершины купола и собственный вес плиты за исключением ребер. Продолжительность действия снеговой нагрузки 90 суток. Нагрузки приводим к кратковременным, используя деформационные n_вр и прочностные k_дс временные коэффициенты, определяемые для неориентированного полиэфирного стеклопластика по рис. 96.

Для постоянно действующей нагрузки от собственного веса элементов находим n_вр = 0,5 и k_дс = 0,22; для снеговой нагрузки при продолжительности ее 90 суток n_вр = 0,52 и k_дс = 0,26.

Результаты подсчета нагрузок сводим в таблицу.

Расчет на изгиб от равнохмерно распределенной по поверхности плиты нагрузки производим по формулам для треугольной в плане пластинки. При расчете рассматриваем пластинку как свободно опертую по контуру с равными сторонами, приняв наибольший размер стороны а = 378 см (рис. 77).

Вычисление прогиба. При вычислении цилиндрической жесткости пластинки учитываем только сечения обшивок, модуль упругости обшивки при эксплуатации в атмосферных условиях Е = 0,8×60 000 = 48 000 кГ/см² (табл. 5,6).

Относительный прогиб в центре пластинки

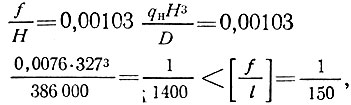
где высота треугольника

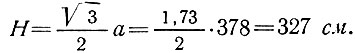
Цилиндрическая жесткость пластинки

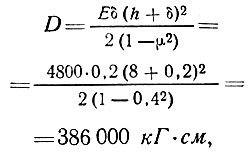
где δ - толщина обшивки;

h - расстояние между обшивками.

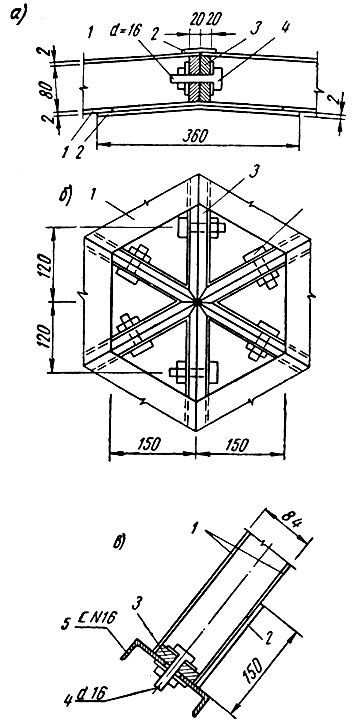
Рис. 83. Стыкование плит и крепление к опорному кольцу: а - поперечное сечение по стыку; б - вид на стык снизу, накладка из стеклопластика не показана; в - крепление плиты к опорному кольцу: 1 - обшивка из стеклопластика; 2 - накладки из стеклопластика; 3 - ребро из однонаправленного стеклопластика; 4 - стальной болт; 5 - опорное кольцо из швеллера

Прогиб плиты, как и следовало ожидать, незначителен, много меньше допускаемого (см. приложение 4).

Проверка прочности по нормальным напряжениям. Расчет на прочность при местном изгибе треугольных плит производим в предположении, что средний слой из колец нормальные напряжения не воспринимает.

Наибольший изгибающий момент в центре пластинки

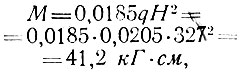
Расчетное сопротивление обшивок изгибу при воздействии атмосферных условий R_и = 0,65×1100 = 715 кГ/см². Находим нормальные напряжения в обшивках и сравниваем их с расчетным сопротивлением

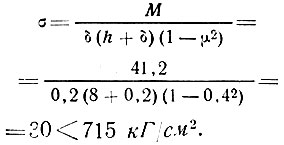
Рис. 84. Монтажный блок из шести плит купола в г. Северо-Донецке

Рис. 85. Начало монтажа купола

Проверка прочности по скалывающим напряжениям по нейтральной плоскости плиты не производится, поскольку швы, между обшивками, ребрами и кольцами имеют большую площадь при очень малых усилиях (см. пример 4).

Соединение плит. На рис. 83 показано примыкание плит, образующих шестигранную пирамиду.

Соединение плит между собой при монтаже осуществляется с помощью стальных болтов диаметром Гб мм, рис. 83, а, б. На каждую сторону при соединении панелей ставится по четыре болта. Предварительно в ребрах просверливаются отверстия для болтов, разметка их производится по кондукторам. Для того чтобы иметь возможность произвести завинчивание гаек болтов, внутренние обшивки плит срезаются у мест постановки болтов. После сборки купола вырезы в нижней обшивке заклеиваются фасонкой из стеклопластика.

Болты предотвращают относительный сдвиг плит и работают на срез и смятие. Ввиду ничтожного значения усилий сдвига S = 89 кГ/м и очевидного запаса прочности, расчет их не производим.

Расчет стального опорного кольца. Опорное кольцо из швеллера № 16 а рассматриваем при расчете как лежащее в одной плоскости с постоянным радиусом r = 14,8 м. Опорами для кольца служат стальные стойки с наибольшим шагом l₁ = l,9 м.

Полный распор от постоянной и снеговой нагрузки согласно рис. 81 равен

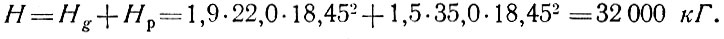
Распор купола на единицу длины кольца

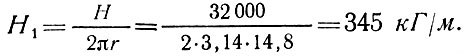
Расчетное растягивающее усилие в кольце

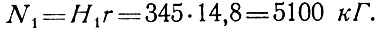
На участке между опорными стойками опорное кольцо изгибается, погонная нагрузка на кольце

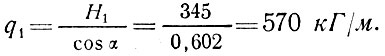
Изгибающий момент в швеллере

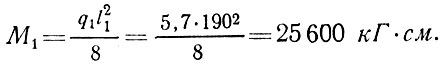
Проверяем швеллер опорного кольца по формуле растянуто изогнутого стержня

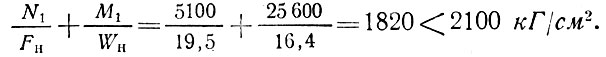
Заключение. Общий вес запроектированного купольного покрытия весьма мал.

Купол подобного типа был построен в 1965 году в г. Северо-Донецке [20, 21]. Монтажный блок купола, состоящий из шести треугольник плит, показан на рис. 84.

Монтаж купола произведен с инвентарных лесов бригадой в составе четырех человеку с помощью крана АК-75 за 56 ч. На рис. 85 показан один из рабочих моментов в начале монтажа купола.